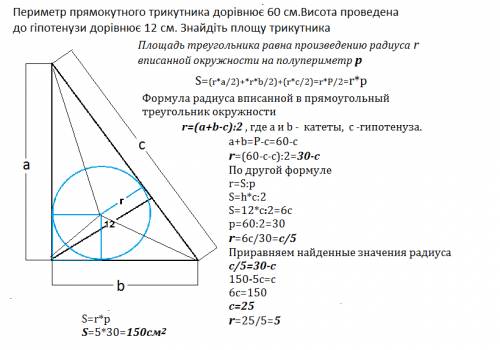
Периметр прямоугольного треугольника равен 60 см. Высота, проведенная к гипотенузе, равна 12 см. Найти площадь треугольника.
* * *
Площадь треугольника равна произведению радиуса r вписанной окружности на полупериметр р
Формула радиуса вписанной в прямоугольный треугольник окружности
r=(a+b-c):2 , где а и b - катеты, c -гипотенуза.
a+b=P-с=60-c
r=(60-c-c):2=30-c
По другой формуле
r=S:p
S=h*c:2
S=12*c:2=6c
р=60:2=30
r=6c/30=c/5
Приравняем найденные значения радиуса
c/5=30-c
150-5c=c
6c=150
c=25 см
r=25/5=5 см
S=r*p=5*30=150 см²
1)3x - 7 < x + 1
2x<8
x<4
2)2 + x > 8 - x
2x>6
x>3
3)1 - x ≤ 2x - 5
-3x≤-6
x≥2
4)2x +1 > x+6
x>5
5)4х + 2 > 3х + 1
6x>4
x>-1
6)6 x+1 < 2х + 9
4x<8
x<2
Пошаговое объяснение: