3)|3-x|<1,2
3-x<1,2, 3-x_>0
-(3-x)<1,2 , 3-x<0
x>18, x<_3
x<4,2, x>3
x£{1,8;3]
x£{3;4,2}
x£{1,8;4,2}
4)|4+x|<1,8
4+x<1,8, 4+x_>0
-(4+x)<1,8, 4+x<0
x<-2,2, x_>-4
x>-5,8, x<-4
x£[-4;-2,2}
x£{-5,8;-4}
x£{-5,8;-2,2}
Пошаговое объяснение:
Что означают эти знаки <_ или _>
<_ это меньше ровно
_> это больше ровно
возможно есть более короткий вариант, но это более развернутое объяснение, я не указывала квадратные сантиметры, но я думаю ты сам(а) знаешь где их поставить
PS лайк, если можно
Пошаговое объяснение:
для начала найдем площадь маленького квадрата на пересечении :
8-4=4. -первая сторона
6-2=4. - вторая сторона
4*4=16см - площадь этого квадрата
(получается это квадрат 4 на 4см)
далее площадь верхнего прямоугольника:
8*16=128см - площадь верхнего
ищем площадь нижнего прямоугольника, для начала надо найти его вторую сторону :
4+4=8см - вторая сторона нижнего прямоугольника
сейчас найдем сам прямоугольник:
8*6=48см - площадь нижнего прямоугольника
теперь складываем площади:
48+128=176см - площадь всей фигуры, но это не конец ТК мы посчитали квадрат на пересечении 2 раза .
отнимаем его площадь :
176-16=160см - ПЛОЩАДЬ ФИГУРЫ
далее периметр:
я это сделаю выражением так удобнее
8+16+4+2+(4+4)+6+4+(16-4)=60см - ПЕРИМЕТР
Поскольку известны корни трехчлена, то верны следующие равенства:
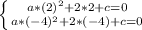
Преобразовываем оба уравнения:
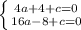
Вычитаем второе из первого:
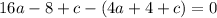
Приводим подобные:
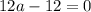, отсюда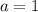 
Подставляем a в одно из уравнений, например, в первое:
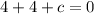, откуда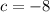 
Тогда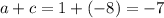 
По теореме Виета, для квадратного уравнения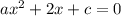 
, если 
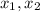- корни уравнения, то верно следующее:
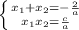
(правая часть первого уравнения - коэффициент при x, деленный на коэффициент при старшей степени, т.е. a, взятый со знаком минус, правая часть второго уравнения - свободный коэффициент, то бишь c, деленный на коэффициент при старшей степени, то бишь a)
Поскольку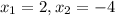 
, то получаем:
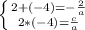
Из первого уравнения находим 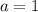. Подставляем a во второе уравнение, находим, что 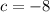. Наконец, находим сумму:
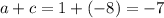
Эпилог
Двумя получили одинаковый результат, и это хорошо.
991. решите нераыенства 3) |3-х|<1,24) |4+х|<1,8