Пошаговое объяснение:
14-10=4(м/с)-скорость сближения
4*25=100(м)-сблизятся за 25 сек
150-100=50(м)-расстояние между ними через 25 сек
ответ: 50 м.
Пошаговое объяснение:
1.
Пусть скорость теплохода по озеру - х,
а скорость течения реки - у.
Принимаем расстояние, которое продходит теплоход за 1. ⇒
{1/х=4 {x=1/4 {x=1/4
{1/(x+y)=3 {x+y=1/3 {(1/4)+y=1/3 {y=(1/3)-(1/4)=(4-3)/12=1/12. ⇒
Скорость теплохода против течения:
x-y=(1/4)-(1/12)=(3-1)/12=2/12=1/6.
Время, за которое теплоход проходит то же расстояние против течения реки: 1/(1/6)=6 (час).
2.
Пусть собственная скорость лодки - х, а скорость течения реки - у.
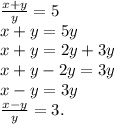
ответ: скорость лодки против течения реки больше скорости
течения реки в 3 раза.
Пошаговое объяснение:
1.
Пусть скорость теплохода по озеру - х,
а скорость течения реки - у.
Принимаем расстояние, которое продходит теплоход за 1. ⇒
{1/х=4 {x=1/4 {x=1/4
{1/(x+y)=3 {x+y=1/3 {(1/4)+y=1/3 {y=(1/3)-(1/4)=(4-3)/12=1/12. ⇒
Скорость теплохода против течения:
x-y=(1/4)-(1/12)=(3-1)/12=2/12=1/6.
Время, за которое теплоход проходит то же расстояние против течения реки: 1/(1/6)=6 (час).
2.
Пусть собственная скорость лодки - х, а скорость течения реки - у.
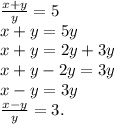
ответ: скорость лодки против течения реки больше скорости
течения реки в 3 раза.
50 м
Так как 14×25=350, а 10×25=250
150+250=400( насколько далеко мышь)
400-350=50(насколько далеко мышь после того как кот бежал вместе с ней
Пошаговое объяснение:
Удачи