а) 48+42*18:63-56 б)36+95-205*48:164 в) (3539+5016-12*203):211
1) 42*18=756 1)205*48=9840 1)12*203=2436
2) 756:63=12 2)9480:164=60 2)3539+5016=8555
3)48+12=60 3)36+95=131 3)8555-2436=6119
4)60-56=4 4)131-60=71 4)6119:211=29
г) (2356+809-2841)*106:159
1)2356+809=3165
2)3165-2841=324
3)324*106=34344
4)34344:159=216
Пошаговое объяснение:
1) строим область допустимых решений. , т.е. решаем графически систему неравенств.
строим каждую прямую и определим полуплоскости, заданные неравенствами
2) где все полуплоскости пересекаются, там и есть наша область допустимых решений
на графике я ее заштриховала, и отметила точки, определяющие "углы" области
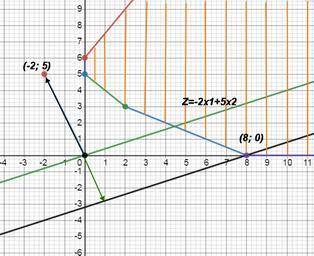
3) теперь целевая функция задачи Z = -2x1+5x2 → min.
нарисуем график Z= -2x1+5x2 (зеленая линия через начало координат) его и будем двигать для поиска решений
вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). начало вектора – точка (0; 0), конец – точка (-2;5), но нам надо минимизация, поэтому прямую
Z = -2x1+5x2 будем двигать по вектору, но в противоположном направлении. (т.е. будем ее параллельным образом двигать вниз) до первого касания обозначенной области
в конце концов, эта прямая дойдет до нижней точки (8;0)
сюда и найдем минимальное значение целевой функции:
Z(x) = -2*8 + 5*0 = -16
ответ: 68 туристов знали два языка
Пошаговое объяснение:
100 - 10 = 90 (языков) - знали разные языки
Пусть количество людей два языка х
Для решения задачи составим уравнение:
х + (83 - х) + (75 - х) = 90
х - х - х + 83 + 75 = 90
-х + 158 = 90
х = 158 - 90
х = 68
ответ: 68 туристов знали два языка