12\5 + 3\5X = 16\15 X + 39\25
3\5X - 16\15X = 39\25 - 12\5
(9\15 - 16\15)X = (39\25 - 60\25)
- 7\15 X = - 21\25
175X = 315
X = 1.8
ответ: 1.8
Возраст волшебника 12087 лет.
Пошаговое объяснение:
Требуется найти пятизначное число, в котором все цифры разные, а трехзначное число, стоящее между крайними цифрами, делится на 13.
1) По условию первая цифра в 7 раз меньше последней. ⇒ Первая цифра в числе не может быть больше единицы, иначе последняя цифра будет двузначной (2*7 = 14) и мы выйдем за рамки пятизначных чисел. ⇒ Первая цифра = 1, последняя цифра = 7.
Исходное число имеет вид 1 * * * 7.
2) Между цифрами 1 и 7 стоит трехзначное число, которое делится на 13. Его можно представить как 13n, n ∈ Z (n - целое число).
По условию в исходном числе все цифры разные, поэтому это трехзначное число не может принадлежать первой сотне трехзначных чисел, так как цифра 1 у нас уже есть. ⇒
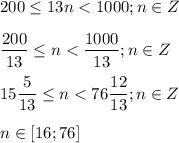
⇒ при n = 16 число 13n = 13*16 = 208. Число 208 наименьшее допустимое трехзначное число, удовлетворяющее условию задачи.
Тогда исходное число 12087.
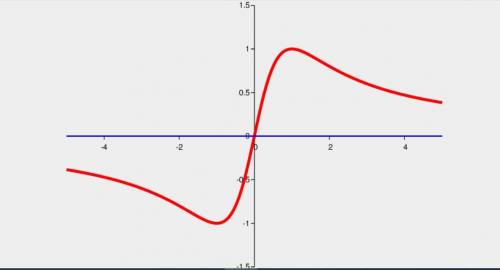
Дана функция y = 2x/(x² + 1.
Функция нечетная.
Условия для точек разрыва : x² + 1 = 0, x² = -1.
Точки разрыва : нет.
Корни функции (точки пересечения с осью абсцисс x) : x = 0.
Вычисление y′ : y′=2⋅1(x²+1)−x(2x)(x²+1)2=2⋅1−x²(x²+1)2=−2(x−1)(x+1)(x2+1)2
Первая производная : y′=−2(x−1)(x+1)/(x²+1)²
Условия для стационарных точек : −2(x−1)(x+1)=0
Стационарные точки : х1=−1, х2=1
Вторая производная : y′′=4x(x²−3)/(x²+1)³
Условия для критических точек : 4x(x²−3)=0
Критические точки : х1=−√3, х2=√3, х3=0
Асимптота на обоих ±∞ линия y=0.
(3/5)х - (11/15)х = 1.56-2.4
(9-11/15)х = 0.84
-(2/15)х = 0.84
х = -6.3