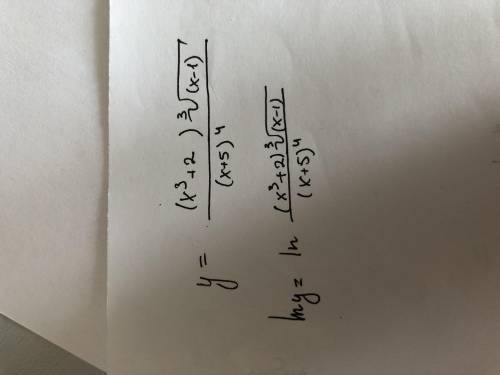
![y = \frac{( {x}^{3} + 2) \sqrt[3]{x - 1} }{ {(x + 5)}^{4} } \\](/tpl/images/1700/3115/3d726.png)
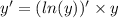
![(ln(y))' = ( ln(( \frac{ ({x}^{3} + 2) \sqrt[3]{x - 1} }{ {(x + 5)}^{4} } )) ' = \\ = ( ln( {x}^{3} + 2) + ln( {(x - 1)}^{ \frac{1}{3} } - ln( {(x + 5)}^{4} ) ) ' = \\ = \frac{3 {x}^{2} }{ {x}^{3} + 2 } + \frac{1}{3} \times \frac{1}{x - 1} - \frac{4}{x + 5} = \\ = \frac{3 {x}^{2} \times 3(x - 1)(x + 5) + ( {x}^{3} + 2)(x + 5) - 4 \times 3(x - 1)( {x}^{3} + 2)}{3( {x}^{3} + 2)(x - 1)(x + 5) } = \\ = \frac{9 {x}^{2}( {x}^{2} + 5x - x - 5) + {x}^{4} + 5 {x}^{3} + 2x + 10 - 12( {x}^{4} + 2x - {x}^{3} - 2) }{3( {x}^{3} + 2)(x - 1)(x + 5) } = \\ = \frac{9 {x}^{4} + 36 {x}^{3} - 45 {x}^{2} + {x}^{4} + 5 {x}^{3} + 2x + 10 - 12 {x}^{4} - 24x + 12 {x}^{3} + 24 }{3( {x}^{3} + 2)(x - 1)(x + 5)} = \\ = \frac{ - 2 {x}^{4} + 53 {x}^{3} - 45 {x}^{2} - 22x + 34 }{3( {x}^ {3} + 2)(x - 1)(x + 5) }](/tpl/images/1700/3115/dd15d.png)
![y' = \frac{( {x}^{3} + 2) \sqrt[3]{x - 1} }{ {(x + 5)}^{4} } \times \frac{ (- 2 {x}^{4} + 53 {x}^{3} - 45 {x}^{2} - 22x + 34) }{3( {x}^ {3} + 2)(x - 1)(x + 5) } = \\ = - \frac{2 {x}^{4} - 53 {x}^{3} + 45 {x}^{2} + 22x - 34}{ \sqrt[3]{ {(x - 1)}^{2} {( x + 5)}^{5} } }](/tpl/images/1700/3115/63b99.png)
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Круг — часть плоскости, ограниченная окружностью.
Радиус — отрезок прямой, соединяющий центр окружности с какой-либо её точкой, а также длина этого отрезка. Обычно обозначается R.
Диаметр — отрезок прямой, соединяющий пару наиболее удаленных друг от друга точек окружности, а также длина этого отрезка. Диаметр всегда проходит через центр окружности. Обычно обозначается D или Ø. Диаметр равен удвоенному радиусу окружности: D = 2R, R = D/2.
Радиус круга: R = √(S/π), где √ — корень квадратный
Диаметр круга: D = 2√(S/π)