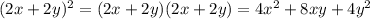Abab 3. В каждом члене двучлена присутствует переменная: (a + 2by. В этом случае можно построить модель, приведённую ниже. (a+2b)= (a + 2b) (a + 2b) = a + 4b + 4ab Изобразите приведённые ниже квадраты двучленов так, как дано в образце, и преобразуйте в трёхчлен: б) (2а + с); в)(х + 3у); г) (2а + 3b); д) (4m+n)2; е) (2x+2y). Б. Б. ab ab ра) (m+n); БРЬ De
Определенные трудности использования защитных сооружений гражданской обороны связаны также с установленным порядком применения их по двойному назначению. Дело в том, что имеющийся фонд этих сооружений независимо от ведомственной принадлежности должен использоваться для хозяйственных, культурных и бытовых нужд без ущерба для выполнения задач по предназначению. Для освобождения защитных сооружений в военное время от размещавшегося в них имущества организаций отводится 12 часов. При чрезвычайных же ситуациях, например, при радиационных и химических авариях, как правило, возникает необходимость занять защитные сооружения в значительно более короткие сроки.
Давайте найдем первообразную F(x) (если она подразумевается). Производная от F(x) - это f(x). Первая часть неравенства меньше нуля, когда f(x)<0, => -2x+3<0 => x > (3/2)
Вторая часть сама первообразная. Давайте найдем нужную (при F(0)=4). F(x) = Где C - аддитивная константа. Решим и это неравенство. При F(0) = C, значит C = 4. Отсюда нужная F(x)= Она же меньше нуля. Решим методом интервалов. Определим, когда F(x)=0. D= Тогда x= x= Составим интервалы. Знаки в интервалах можно определить, просто подставляя значения из них в ф-ию. (-inf;-1)<0 (-1;4)>0 (4;+inf)<0 Нам, судя по нер-вам, нужны <0, значит подходят (-inf;-1)u(4;+inf) Теперь объединим. Не указано "И" или "ИЛИ" поэтому сделаю оба варианта. Если "И" (фигурные скобки) x принадлежит (4;+inf). Если "ИЛИ" (квадратные скобки) x принадлежит (-inf;-1)u(3/2;+inf).
ответ: во
Пошаговое объяснение:
а)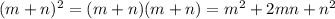
б)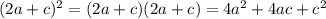
в)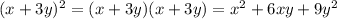
г)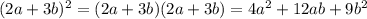
д)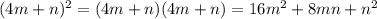
е)