целыми числами являются -8;0;3;-4
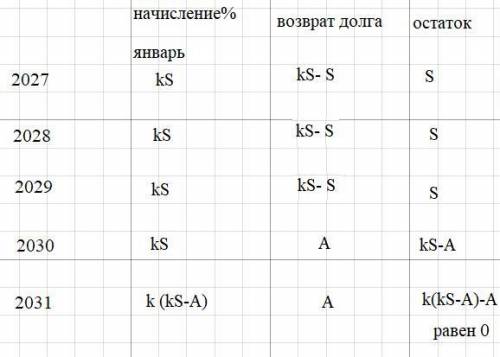
Cумма кредита S=220 тыс руб.
Каждый январь начисляются проценты на остаток.
r%= 0,01·r
Обозначим
1+0,01·r= k
( cм схему начисления и остатки к таблице)
Уравнение 1:
k·(kS–A)–A=0
Уравнение 2:
3·(kS–S)+2A=420
S=220
Решаем систему уравнений:
{k(220k−A)−A=03(220k−220)+2A=420
{220k2=A(k+1)660k−660+2A=420
⎧⎩⎨A=220k2k+1660k+2220k2k+1=1080 {A=220k2k+166k(k+1)+44k2=108(k+1)
{A=220k2k+155k2−21k−54=0 D=212–4·55·(–54)=441+11880=12321=1112
k=1,2 второй корень отрицательный
1+0,01r=k ⇒ 1+0,01r=1,2 ⇒ 0,01·r=0,2 ⇒ r=20%
О т в е т. 20%
___
Поскольку числа 49 и 9 взаимно простые, тоесть не имеют общих делителей, кроме числа 1, то для того, чтобы некоторое число было кратным одновременно 49 и 9, необходимо, чтобы это число было кратным произведению чисел 49 и 9.
Всякое число х, кратное произведению чисел 49 и 9 можно записать в виде х = 49 * 9 * k, где k — некоторое целое число.
Перебирая значения k, начиная от k = 1, найдем все трехзначные числа, которые можно представить в виде 49 * 9 * k.
При k = 1 получаем х = 49 * 9 * 1 = 441.
При k = 2 получаем х = 49 * 9 * 2 = 882.
При k = 3 получаем х = 49 * 9 * 3 = 1323.
Следовательно, начиная с k = 3 число знаков в записи чисел вида 49 * 9 * k становится больше трех.
Следовательно, существует 2 трехзначные числа, кратные одновременно 49 и 9 : 441 и 882.
Их сумма равна: 441 + 882 = 1323.
ответ:1323.
-8;0;3;-4