В правильной пирамиде медиана боковой грани к основанию - это апофема А.
Сторона основания а и основание боковой грани а равны по 1.
Находим апофему: A = 2S/a = 2*1/1 = 2.
По свойству медиан точка М делит апофему в отношении 2:1 от вершины. SM = (2/3)*2 = 4/3, МК = (1/3)*2 = 2/3.
Находим высоту пирамиды: H = √(2² - (1/2)²) = √15/2.
Находим косинус и синус угла α между основанием пирамиды и боковой гранью.
cos α = (1/2)/2 = 1/4, sin α = (√15/2)/2 = √15/4.
Косинус угла при вершине пирамиды (назовём его S) равен:
cos S = (22 + 22 – 12)/(2*2*2) = 7/8, синус равен √(1 – (49/64)) = √15/8.
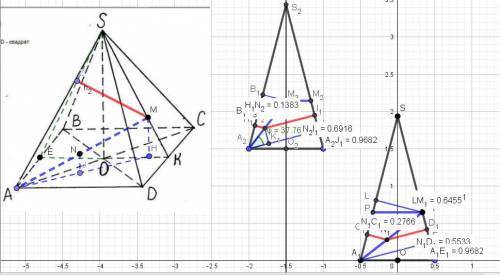
Проведём два осевых сечения пирамиды перпендикулярно смежным сторонам основания и спроецируем на эти плоскости точки M и N (они даны на прилагаемых рисунках).
Расстояния от точек М и N до граней пирамиды обозначим буквой h.
До основания: h(М) = (1/3) H = (1/3)*(√15/2) = √15/6.
h(N) = (3/7) hM = (3/7)*(√15/6) = √15/14.
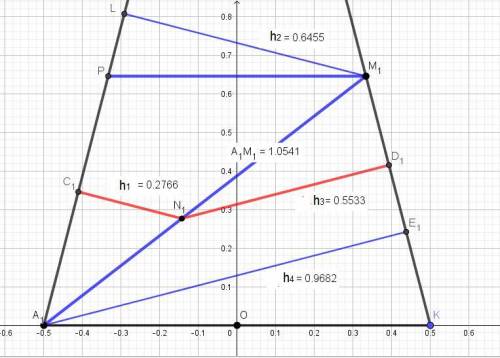
До грани, содержащую точку М, и противоположную ей.
Высота h2 = SM*sin S = (4/3)*(√15/8) = √15/6.
h1 = (3/7) h2 = (3/7)*(√15/6) = √15/14.
Высота h4 = a*sin α = 1*(√15/4) = √15/4.
h3 = (4/7) h4 = (4/7)*(√15/4) = √15/7.
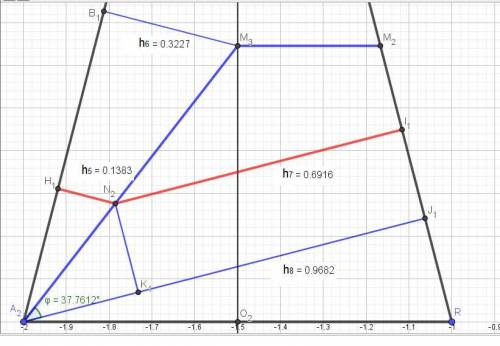
Рассмотрим второе сечение.
Высота h6 = SM3*sin (S/2) = (2/3)*H*((1/2)/2) = (2/3)*(√15/2)*(1/4) = √15/12.
h5 = (3/7) h6 = (3/7)*(√15/12) = √15/28.
Высота h8 = a*sin α = 1*(√15/4) = √15/4.
Для определения высоты h7 найдём угол φ.
φ = arc tg(M3O/(a/2)) – (90º - arc sin α) = arc tg((√15/6)/(1/2)) – arc sin(√15/4) = arc tg((√15/3) – arc sin(√15/4) = 52,23875609º – (90º - 75,52248781º) =
= 37,76124391º.
cos φ = 0,790569.
Найдём длину проекции отрезка АМ на секущую плоскость SEK по теореме косинусов: AM = √(12 + (2/3)² - 2*1*(2/3)*(1/4)) = √(1 + (4/9) – (1/3)) = √10/3.
Тогда AN = (3/7)AM = (3/7)*( √10/3) = √10/7.
Отсюда h7 = h8 – AN*cos φ = √15/4 – (√15/7)*0,790569 = 0,691604.
Сложим длины всех заданных высот:
Σh = (√15/14) + (√15/14) + (√15/7) + (√15/28) + 0,691604 = 1,936492.
Пошаговое объяснение:
y=5x-2 y=5x-2 y=5x-2
4x+5y+4=0 y=(-4x-4)/5 y=-4x/5-4/5
а) 5x-2=-4x/5-4/5
5x+4x/5=-4/5+2
29x/5=6/5
x=6/29 y=5*(6/29)-2=30/29-58/29=-28/29
Точка пересечения прямых (6,29;-28.29)
б) угол между прямыми можно найти по формуле
tgφ=(k₂-k₁)/(1+k₁k₂)
где k₁ и k₂ угловые коэффициенты, в наших уравнения они равны
k₁=5; k₂=-4/5
Проверим будут ли прямые перпендикулярны (условие перпендикулярности прямых 1+k₁k₂=0):
1+5*(-4/5)=1-4=-3≠0 - значит прямые не перпендикулярны
Подставляем значения коэффициентов в формулу нахождения угла:
tgφ=(-4/5-5)/-3=29/15
φ=arctg(29/15) ≈ 1,0934 рад ≈ 63°
Y=5x-2 y=5x-2 y=5x-2
4x+5y+4=0 y = (-4x-4) / 5 y=-4x/5-4/5
а) 5x-2=-4x/5-4/5
5x+4x/5=-4/5+2
29x/5=6/5
x=6/29 y=5 * (6/29) - 2=30/29-58/29=-28/29
Точка пересечения прямых (6,29;-28.29)
б) угол между прямыми можно найти по формуле
tgφ = (k2-k1) / (1+k1k2)
где k1 и k2 угловые коэффициенты, в наших уравнения они равны
k1=5; k2=-4/5
Проверим будут ли прямые перпендикулярны (условие перпендикулярности прямых 1+k1k2=0) :
1+5 * (-4/5) = 1-4=-3≠0 - значит прямые не перпендикулярны
Подставляем значения коэффициентов в формулу нахождения угла:
tgφ = (-4/5-5) / - 3=29/15
φ=arctg (29/15) ≈ 1,0934 рад ≈ 63° 5x - 2 = -0,8x - 0,8;
5x + 0,8x = 2 - 0,8;
5,8x = 1,2;
x = 1,2 / 5,8 = 12/58 = 6/29.
y = 5x - 2 = 5 * 6/29 - 2 = 30/29 - 58/29 = -28/29.
(x; y) = (6/29; -28/29). tg(α1) = k1 = 5;
tg(α2) = k2 = -0,8;
tgα = |tg(α1 - α2)|;
tgα = |(tg(α1) - tg(α2)) / (1 + tg(α1)tg(α2))|;
tgα = |(k1 - k2) / (1 + k1k2)|;
tgα = |(5 + 0,8) / (1 - 5 * 0,8)|;
tgα = |5,8 / (-3)| = 29/15;
α = arctg(29/15).
а) точка пересечения прямых: (6/29; -28/29);
14^cosx-2^cosx*7^-sinx=0
2^cosx*7^cosx-2^cosx*7^-sinx=0
2^cosx(7^cosx-7^-sinx)=0
2^cosx=0 или 7^cosx=7^-sinx
в первом решений нет
cosx=-sinx
x=3pi/4+pi*n, n принадлежит Z
в промежутке ответ 3pi/4