Для решения выражения 815 * 204 - (8963 + 68077) : 36; 9676 + 12237 - 8787 * 2 : 29 необходимо выполнить по четыре действия.
Решение примера:
1) 815 * 204 - (8963 + 68077) : 36 = 166260 - 77040 : 36 = 166260 - 2140 = 164120;
1) 8963 + 68077 = 77040,
2) 815 * 204 = 166260,
3) 77040 : 36 = 2140,
4) 166260 - 2140 = 164120.
2) 9676 + 12237 - 8787 * 2 : 29 = 9676 + 12237 - 606 = 21913 - 606 = 21307.
1) 8787 * 2 = 17574,
2) 17574 : 29 = 606,
3) 9676 + 12237 = 21913,
4) 21913 - 606 = 21307.
ответ примера: 164120; 21307.
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная. Нет деления на ноль.
2. Пересечение с осью Х. Y= x²*(x+9) при х = 0,0, 9
Положительна - во всем интервале..
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.limY(-∞) = + ∞ limY(+∞) = -∞
Горизонтальной асимптоты - нет.
5. Исследование на чётность.Y(-x) ≠ - Y(x).
Функция ни чётная ни нечётная - общего вида.
6. Производная функции.Y'(x)= -3*x² +18*х = -3*х*(x-6).
Корни при Х= 0 и 6.
(-∞)__(<0-убыв)__(0)___(>0-возр)___(6)__(<0-убыв)_____(+∞)
7. Локальные экстремумы.
Максимум Ymax(6)= 108 , минимум – Ymin(0)=0.
8. Интервалы возрастания и убывания.
Возрастает - между корнями - Х∈[0;6], убывает = Х∈(-∞;0]∪[6;+∞).
8. Вторая производная - Y"(x) = -6*x + 18= -6*(х -3)=0.
Корень производной - точка перегиба Y"(x)= 0 при х=3.
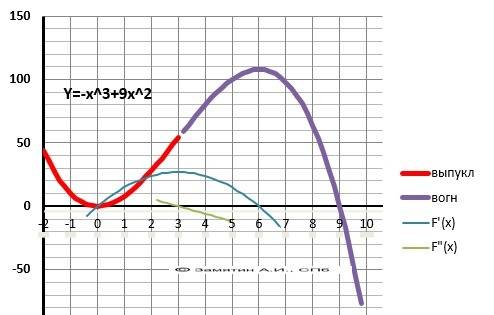
9. Выпуклая “горка» Х∈(3;+∞), Вогнутая – «ложка» Х∈(-∞;3).
10. График в приложении.
Сумма чисел -19 и 21 будет больше
Пошаговое объяснение:
Если правильно понял, что спрашивают. Сумма двух отрицательных чисел будет отрицательным числом, а сумма отрицательного -19 и положительного 21 будет положительным числом