вот это подойдет надеюсь?
1) 1/2m = 0.5m = 50cm 50cm < 60cm 2) 1/4 сут. = 0.25 сут. = 6 ч 6ч < 12ч 3) 1/4 сут. = 0.25 сут. = 6ч = 360 мин 360 мин > 340 мин 4) 1/5 м = 0.2 м = 2 дм 2дм < 200дм 5) 1/2 сут. = 0.5 сут = 12 ч 12ч = 12ч 6) 1/4 м < 1/2м ( Представь, что у тебя в руках торт, в первой дроби у тебя только 1 кусочек из 4 , а от другого торта сразу половина, следовательно 1/2 больше) 7) 1/4ц = 0.25ц = 25 кг 25кг = 25кг 8) 1/2 ч = 0.5 ч = 30 мин 30 мин < 35 мин 9) 1/3 ч = 20 мин 20 мин < 50 мин
Если что я не знаю
Пошаговое объяснение:
Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!. Используя эту формулу, решается задача 1) и 2) - ответами в обоих будет число 24. Для задачи 3) введем формулу (на картинке), где m - количество элементов в конечной выборке (т.е. то кол-во мужчин, которые садятся на скамейку), а n - кол-во элементов массива(кол-во свободных на скамейке мест). Подставив все величины в формулу, получим :
C =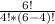 
= 15 возможностей их различной посадки
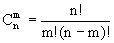
30:4=7( ост. 2) 4*7+2=28+2=30
10:3=3(ост. 1) 3*3+1=9+1=10
35:6=5(ост.5) 6*5+5=30+5=35
20:7=2(ост.6) 2*7+6=14+6=20
60:9=6(ост.6) 6*9+6=54+6=60
60:8=7(ост.4) 7*8+4=56+4=60
50:8=6(ост.2) 6*8+2=48+2=50
17:3=5(ост.2) 5*3+2=15+2=17