Раз, два.
Мы не ели,
Три, четыре.
Есть хотим!
Открывайте шире двери, а то повара съедим!
Все столы перевернём!
И Довольные уйдём
Нам покушать очень нужно,
Чтобы нам шагать по лужам
Мы готовы тихо сесть
Только б дали нам поесть
Мы поели, мы попили,
Червячка мы заморили,
Мы пойдём, передохнём
И опять поесть придём!
p.s. поблагодарить за еду нужно, и вот такой кричалкой можно это сделать:
нашим поварам
За макароны и сырок,
За помидоры и чаёк.
7.
Из обратно теоремы о пропорциональных отрезков, если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные или пропорциональные между собой отрезки, начиная от вершины, то такие прямые параллельны. Отсюда следует, что:
Отрезки MN и NK параллельны отрезкам BC и AD, а значит, и весь отрезок MK || основам трапеции (BC || AD). MK — средняя линия трапеции, т.к. точка М делит сторону AB пополам.
Формула для нахождения ср. линии трапеции:
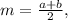
где a и b — основы трапеции.
Подставляем значения:
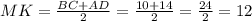
ответ: MK = 12.
8. EM || BC || AD по теореме о пропорциональных отрезках. EM — средняя линия трапеции. Все отрезки, образующие среднюю линию EM параллельны основам трапеции.
Найдем EM:
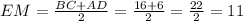
Средняя линия делит диагонали пополам.
Р-м ΔABC и ΔDCC: EK и LM — средние линии.
Средняя линия треугольника равна половине стороны к которой она параллельна. Находим длины этих отрезков.
EK = LM = DB/2 = 6/2 = 3.
Находим KL: EM − (EK+LM) = 11−(3+3) = 5
ответ. KL = 5.
9. ABCD — равнобедренная трапеция. MF — средняя линия, AM = MB = CF = FD = 2. BC = EK = 2. BE и CK — высоты трапеции.
Р-м прямоугольные треугольники ABE и DKC: ∠A = ∠D = 60°. Значит ∠AEB и ∠KCD — по 30°.
Катет, лежажий напротив угла, синус которого 30°, равен половине гипотенузе. AE/KD = AB/CD/2= 2.
AD = 2*2+2 = 6
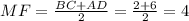
ответ: MF = 4.
бегали мы и скакали
очень очень все устали!
подкрепимся,отдохнем
и опять играть(гулять)пойдем!