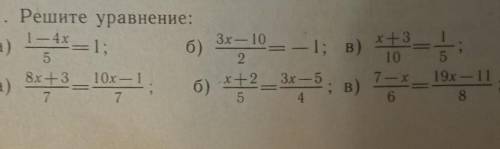
Пошаговое объяснение:
Уравнения, выглядящие наподобие ax^2 + bx + c = 0, называются квадратными. Под буквами a, b, c подразумеваются числа, x - это пока неизвестное число. a - это первый коэффициент, b - второй, а c - свободный член.
Первый коэффициент стоит перед x^2. Он равен:
a = 1.
Второй коэффициент стоит перед x. Он равен:
b = 0.
Свободный член - это число, который стоит без x:
c = -7.
Под дискриминантом понимают число, которое равно b^2 - 4ac: D = b^2 - 4ac = 0^2 - 4 * 1 * -7 = 28.
Дискриминант ищут для того, чтобы узнать сколько решений у квадратного уравнения. Решение - это какие числа можно поставить вместо неизвестного числа, чтобы получить верное равенство. Итак найдём дискриминант:
D > 0, значит решений два: x = (-b ± D^(1/2))/(2a).
D^(1/2) = 28^(1/2).
x1 = 28^(1/2) / 2.
x2 = -28^(1/2) / 2.
за вопрос
вот мое решение:
а)
(1-4x)/5 = 1
1 - 4x = 5
-4x = 4
x = -1
б)
(3x-10)/2 = -1
3x-10 = -2
3x = 8
x = 8/3 = 2 целых и 2/3
в)
(x+3)/10 = 1/5
x+3 = 2
x = -1
а)
(8x+3)/7 = (10x-1)/7
8x+3 = 10x-1
-2x = -4
x = 2
б)
(x+2)/5 = (3x-5)/4
(x+2)*4 = (3x-5)*5
4x + 8 = 15x - 25
-11x = -17
x = -17/(-11) = 17/11 = 1 целая и 6/11
в)
(7-x)/6 = (19x-11)/8
(7-x)*8 = (19x-11)*6
56 - 8x = 114x - 66
-122x = -122
x = 1
Надеюсь