нет не правильно там 117
Пошаговое объяснение:
0
Пошаговое объяснение:
В исходном уравнении первые два слагаемых делятся на 2, значит и третье должно делиться на два. Тогда сделаем замену переменных
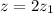
Получится уравнение
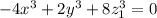
Сократим на 2:
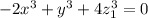
Перепишем немного в другом виде:
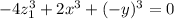
Мы получили в точности исходное уравнение, но в других переменных:
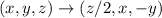
(причем z/2 - целое). Произведем такую замену трижды:
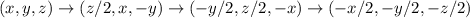
Получили уравнение
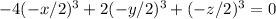
Или
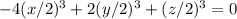
Таким образом числа x/2, y/2, z/2 должны быть целыми, то есть x, y, z должны делиться на 2.
Выполнив эту процедуру еще раз, мы докажем, что x/4, y/4, z/4 целые, т.е. x, y, z делятся на 4. Продолжая дальше мы докажем, что x, y, z должны делиться на весь ряд степеней двойки. Но на него делится только 0. А значит x, y, z все обязаны быть нулями. Тогда величина
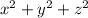
может принимать только нулевые значения.
ответ: y=√[-2*x²-2*x-1+C*e^(2*x)]
Пошаговое объяснение:
Разделив обе части уравнения на y, получим уравнение y'-y=2*x²/y. Это есть уравнение Бернулли вида y'+p(x)*y=f(x)*y^n, где p(x)=-1, f(x)=2*x² и n=-1. Произведём замену переменной по формуле z=y^(1-n)=y². Отсюда y=√z, y'=z'/(2*√z) и уравнение принимает вид z'/(2*√z)-√z-2*x²/√z=0. Умножая его на 2*√z, получаем линейное уравнение относительно z: z'-2*z-4*x²=0. Полагая z=u*v, где u и v - неизвестные пока функции от x, получаем уравнение u'*v+u*v'-2*u*v-4*x²=0, которое запишем в виде v*(u'-2*u)+u*v'-4*x²=0. Так как одной из функций u или v мы можем распорядиться по произволу, то поступим так с u и потребуем выполнения условия u'-2*u=0. Решая это дифференциальное уравнение, найдём u=e^(2*x). Подставляя это выражение в уравнение u*v'-4*x²=0, получим уравнение v'=dv/dx=4*x²*e^(-2*x). Отсюда dv=4*x²*e^(-2*x)*dx и, интегрируя, находим v=-2*x²*e^(-2*x)-2*x*e^(-2*x)-e^(-2*x)+C, где C - произвольная постоянная. Тогда z=u*v=-2*x²-2*x-1+C*e^(2*x) и y=√z=√[-2*x²-2*x-1+C*e^(2*x)]. Проверка: y'=[-4*x-2+2*C*e^(2*x)]/{2*√[-2*x²-2*x-1+C*e^(2*x)]}, y*y'=-2*x-1+C*e^(2*x), y²+2*x²=-2*x²-2*x-1+C*e^(2*x)+2*x²=-2*x-1+C*e^(2*x), y*y'=y²+2*x² - получено исходное уравнение - значит, решение найдено верно.
А
1 действие 432 - 18 равно 424
2 424 / 2 равно 212
3 212 + 18 равно 230