Бесконечной периодической десятичной дробью называют такую дробь, десятичные знаки которой, начиная с некоторого, представляют собой повторение одной и той же группы цифр, состоящей или из одной цифры, отличной от 0 и 9, или из нескольких цифр, причем последовательность цифр при повторении в этой группе не изменяется.
Повторяющаяся группа цифр называется периодом бесконечной периодической десятичной дроби.
Для обозначения периода десятичной дроби используют круглые скобки.
Например,
2,616161… = 2,(61) ; 53222222… = 5,3(2) .
Замечание. Еще раз подчеркнем, что период бесконечной десятичной дроби не может состоять из одной или нескольких цифр 0 и не может состоять из одной или нескольких цифр 9.
Бесконечная десятичная дробь, не являющаяся периодической, называется непериодической.
Рассмотрим треугольник одна вершина которого совпадает с вершиной пирамиды, а две другие - середины противолежащих сторон основания
SA = SB * sin ABS
SB = AB / cos ABS
AB = OB * cos ABO
OB = AO / sin ABO
учитывая, что AO = 1 по условию
AB = 2 (половина стороны основания)
2 = AB = OB * cos ABO = (AO / sin ABO) * cos ABO = cos ABO / sin ABO
или cos ABO = 2 sin ABO
угол ABS в два раза больше ABO. Поэтому по формулам преобразования двойных углов получим
SA = SB * sin ABS = (AB / cos ABS) * sin ABS =
= (2 / (cos^2 ABO - sin^2 ABO)) * 2 sin ABO cos ABO =
(подставим здесь формулу cos ABO = 2 sin ABO)
= 4 sin ABO (2 sin ABO) / (4 sin^2 ABO - sin^2 ABO) =
=8 sin^2 ABO / (3 sin^2 ABO) = 8/3
Объем пирамиды равен 1/3 hS = 1/3 * 8/3 * 4*4 = 128/9 = 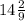
y-x=3 (1)
x=2 (2)
5x+6y=-26 (3)
Найдём точки пересечения (1) и (2): y-2=3; y=5, т.е. получили точку (2;5)
Найдём точки пересечения (3) и (2): 10+6y=-26; 6y=-36; y=-6, получили точку (2;-6)
Найдём точки пересечения (3) и (1): y-x=3 => y-x-3=0 => 6y-6x-18=0
5x+6y=-26 => 5x+6y+26=0
6y-6x-18=5x+6y+26 => -6x-5x=26+18 => -11x=44 => x=-4
y-(-4)=3 => y+4=3 =>y=-1
Точка пересечения: (-4;-1)
Полученная фигура является треугольником. Расстояние от вершины (-4;-1) до прямой х=2 (параллельной оси ординат) составляет: 2-(-4)=6 (высота)
Длина основания треугольника равна: 5-(-6)=11
Площадь треугольника равна: 6*11/2=33