Математика: Найди и исправь ошибки допущенные Незнайкой:

Найди и исправь ошибки допущенные Незнайкой:

👇

Увидеть ответ

Ответ:

Kristina052602

17.09.2021

В первом должно быть восемь

Пошаговое объяснение:

4,6(56 оценок)

Ответ:

MeXaHuK0

17.09.2021

Вот так будет правильно
Найди и исправь ошибки допущенные Незнайкой:

4,4(13 оценок)

Открыть все ответы

Ответ:

Cocos228

17.09.2021

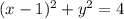
(x-1)^2+y^2=4

Рассмотрим полуокружность, расположенную в верхней полуплоскости. Для нее выразим у:

y^2=4-(x-1)^2

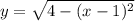
$y=\sqrt{4-(x-1)^2}$

Необходимо найти касательную к графику функции 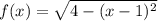$f(x)=\sqrt{4-(x-1)^2}$ , проходящую через точку $(4;\ 0)$ .

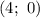Пусть 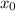x_0 - точка касания. Уравнение касательной:

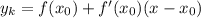
y_k=f(x_0)+f'(x_0)(x-x_0)

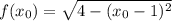
$f(x_0)=\sqrt{4-(x_0-1)^2}$

Найдем производную:

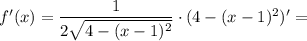
$f'(x)=\dfrac{1}{2\sqrt{4-(x-1)^2}} \cdot(4-(x-1)^2)'=$

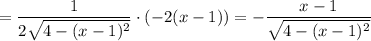
$=\dfrac{1}{2\sqrt{4-(x-1)^2}} \cdot(-2(x-1))=-\dfrac{x-1}{\sqrt{4-(x-1)^2}}$

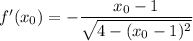
$f'(x_0)=-\dfrac{x_0-1}{\sqrt{4-(x_0-1)^2}}$

Подставим все величины в уравнение касательной:

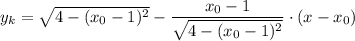
$y_k=\sqrt{4-(x_0-1)^2}-\dfrac{x_0-1}{\sqrt{4-(x_0-1)^2}}\cdot(x-x_0)$

Поскольку касательная проходит через точку 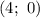$(4;\ 0)$ , то подставим координаты этой точки в уравнение:

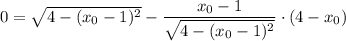
$0=\sqrt{4-(x_0-1)^2}-\dfrac{x_0-1}{\sqrt{4-(x_0-1)^2}}\cdot(4-x_0)$

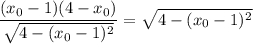
$\dfrac{(x_0-1)(4-x_0)}{\sqrt{4-(x_0-1)^2}}=\sqrt{4-(x_0-1)^2}$

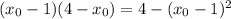
(x_0-1)(4-x_0)=4-(x_0-1)^2

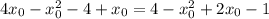
4x_0-x_0^2-4+x_0=4-x_0^2+2x_0-1

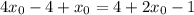
4x_0-4+x_0=4+2x_0-1

3x_0=7

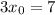
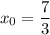
$x_0=\dfrac{7}{3}$

Значит, уравнение касательной имеет вид:

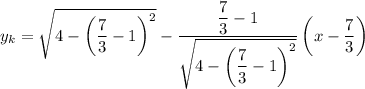
$y_k=\sqrt{4-\left(\dfrac{7}{3} -1\right)^2}-\dfrac{\dfrac{7}{3}-1}{\sqrt{4-\left(\dfrac{7}{3}-1\right)^2}}\left(x-\dfrac{7}{3}\right)$

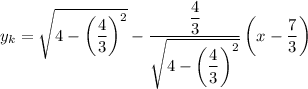
$y_k=\sqrt{4-\left(\dfrac{4}{3}\right)^2}-\dfrac{\dfrac{4}{3}}{\sqrt{4-\left(\dfrac{4}{3}\right)^2}}\left(x-\dfrac{7}{3}\right)$

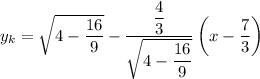
$y_k=\sqrt{4-\dfrac{16}{9}}-\dfrac{\dfrac{4}{3}}{\sqrt{4-\dfrac{16}{9}}}\left(x-\dfrac{7}{3}\right)$

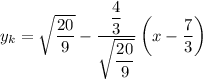
$y_k=\sqrt{\dfrac{20}{9}}-\dfrac{\dfrac{4}{3}}{\sqrt{\dfrac{20}{9}}}\left(x-\dfrac{7}{3}\right)$

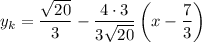
$y_k=\dfrac{\sqrt{20} }{3}-\dfrac{4\cdot3}{3\sqrt{20} }\left(x-\dfrac{7}{3}\right)$

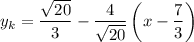
$y_k=\dfrac{\sqrt{20} }{3}-\dfrac{4}{\sqrt{20} }\left(x-\dfrac{7}{3}\right)$

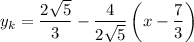
$y_k=\dfrac{2\sqrt{5} }{3}-\dfrac{4}{2\sqrt{5} }\left(x-\dfrac{7}{3}\right)$

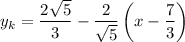
$y_k=\dfrac{2\sqrt{5} }{3}-\dfrac{2}{\sqrt{5} }\left(x-\dfrac{7}{3}\right)$

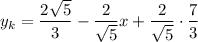
$y_k=\dfrac{2\sqrt{5} }{3}-\dfrac{2}{\sqrt{5} }x+\dfrac{2}{\sqrt{5} }\cdot\dfrac{7}{ 3}\right)$

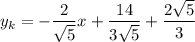
$y_k=-\dfrac{2}{\sqrt{5} }x+\dfrac{14}{3\sqrt{5} }+\dfrac{2\sqrt{5} }{3}$

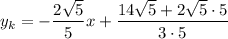
$y_k=-\dfrac{2\sqrt{5} }{5 }x+\dfrac{14\sqrt{5}+2\sqrt{5}\cdot5 }{3\cdot5 }$

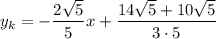
$y_k=-\dfrac{2\sqrt{5} }{5 }x+\dfrac{14\sqrt{5}+10\sqrt{5}}{3\cdot5 }$

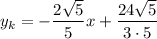
$y_k=-\dfrac{2\sqrt{5} }{5 }x+\dfrac{24\sqrt{5}}{3\cdot5 }$

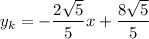
$y_k=-\dfrac{2\sqrt{5} }{5 }x+\dfrac{8\sqrt{5}}{5 }$

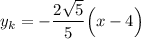
$y_k=-\dfrac{2\sqrt{5} }{5 }\Big(x-4\Big)$

Полуокружность 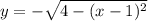$y=-\sqrt{4-(x-1)^2}$ , расположенная в нижней полуплоскости, симметрична относительно рассмотренной относительно оси абсцисс. Значит и касательная к ней будет симметрична:

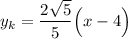
$y_k=\dfrac{2\sqrt{5} }{5 }\Big(x-4\Big)$

Таким образом, две касательные задаются уравнением:

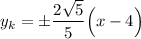
$y_k=\pm\dfrac{2\sqrt{5} }{5 }\Big(x-4\Big)$

4,4(8 оценок)

Ответ:

filimonovajulia1

17.09.2021

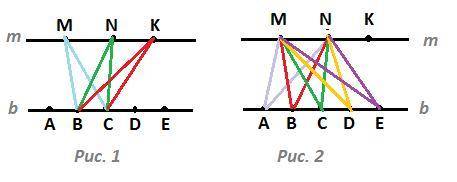
Для построения треугольника нужно взять 3 точки. Эти точки не могут лежать на одной прямой. Чтобы построить треугольник, нужно брать две точки на одной прямой и одну точку на другой.

Рис. 1. На прямой b отмечено 5 точек. Первую точку можно выбрать вторую точку можно выбрать из 4 оставшихся. Так как для треугольника не важно, в каком порядке выбраны вершины, пары точек А,В и В,А равнозначны. Тогда всего вариантов выбрать 2 точки из 5

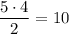
$\dfrac{5\cdot 4}2=10$

Либо по формуле сочетаний 2 из 5

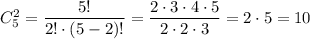
$C_5^2=\dfrac {5!}{2!\cdot (5-2)!}=\dfrac{2\cdot 3\cdot4\cdot5}{2\cdot2\cdot3}=2\cdot5=10$

Для каждой пары точек на прямой b, например, для пары В,С, можно выбрать одну из трёх точек, отмеченных на прямой m. Получится 3 треугольника : ΔBCM, ΔBCN, ΔBCK.

Всего треугольников из 2 точек на прямой b и одной точки на прямой m можно построить 10 · 3 = 30.

Рис. 2. На прямой m отмечено 3 точки. Выбрать две из них можно тремя или M,K или N,K. Для каждой пары можно подобрать одну из пяти точек, отмеченных на прямой b. На рисунке показаны треугольники для пары точек M,N.

Всего треугольников из двух точек на прямой m и одной точки на прямой b можно построить 3 · 5 = 15.

30 + 15 = 45

ответ : 45 треугольников