Треугольник со сторонами 10, 17, 21. вращается вокруг большей стороны. определить объем и поверхность полученного тела

👇

Ответ:

Vs94ski

02.06.2023

Тело, которое получилось, имеет веретенообразную форму: два конуса с одним общим основанием,
радиус r которого - высота ВО треугольника АВС, проведенная к стороне АС, вокруг которой треугольник вращается;
образующие - АВ и ВС соответственно;
высота каждого конуса - СО и ОА, сумма которых равна АС.
Объем тела вращения равен сумме объемов конусов:
V=v₁ +v₂
v₁=Sh₁:3=πr²h₁:3
v₂=Sh₂:3=πr²h₁:3
V=πr²h₁:3+πr²h₁:3=S(h₁+h₂):3=πr²*АС:3

Радиус r основания, общего для обоих конусов, найдем из площади треугольника АВС, найденной по формуле Герона.

Вычисления банальны, приводить поэтому иx не буду.
Площадь треугольника АВС равна 84
r=ВО=2S ᐃ АВС:АС=168:21=8
V =πr²*АС:3=π*64*21:3=448π
Площадь поверхности равна сумме площадей боковой поверхности конусов:
Sт.вр.=πrL₁+πrL₂=πr(L₁+L₁)
Sт.вр.=π*8*(10+17)=216π

Треугольник со сторонами 10, 17, 21. вращается вокруг большей стороны. определить объем и поверхност

4,4(11 оценок)

Открыть все ответы

Ответ:

AXMED2001

02.06.2023

Не совсем понял задание,а в частности табличку,поэтому сугубо по задаче:

Цех кол-во за День Время ВСЕГО

1-й цех ? 18 Дней 1800 кост

2-й цех ? 9 Дней 1800 кост

Пошаговое объяснение:

1. 1800 : 18 = 100 (костюмов за день)

2. 1800 : 9 = 200 (костюмов за день)

3. 200 + 100 = 300 (общая выработка костюмов)

4. 1800 : 300 = 6 (дней)

ответ: за 6 дней общей выработки двух цехов получиться закрыть план в 1800 костюмов.

4,7(95 оценок)

Ответ:

Vadim55554

02.06.2023

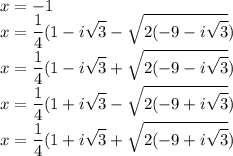
$\displaystyle x=-1\\x=\frac14(1-i\sqrt3-\sqrt{2(-9-i\sqrt3})\\x=\frac14(1-i\sqrt3+\sqrt{2(-9-i\sqrt3})\\x=\frac14(1+i\sqrt3-\sqrt{2(-9+i\sqrt3})\\x=\frac14(1+i\sqrt3+\sqrt{2(-9+i\sqrt3})$

Пошаговое объяснение:

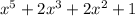
x^5+2x^3+2x^2+1

Подставим вместо х -1. Тогда получим

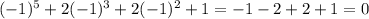
(-1)^5+2(-1)^3+2(-1)^2+1=-1-2+2+1=0

Тогда х = -1 корень данного многочлена. Тогда этот многочлен можно представить в виде 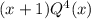(x+1)Q^4(x) , где Q - многочлен 4 степени. Найдём Q

Так как многочлен симметричный, то и Q будет симметричным. (это верно потому, что при раскрытии скобок данный многочлен будет иметь одинаковые коэффициенты везде, где у исходного были одинаковые коэффициенты)

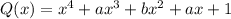Q(x)=x^4+ax^3+bx^2+ax+1 (симметричный многочлен)

Умножим его на (x+1) и найдем a и b

$a=-1\\b=3$

Тогда

Q(x)=x^4-x^3+3x^2-x+1

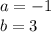
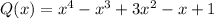
Тогда, чтобы найти корни многочлена 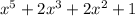x^5+2x^3+2x^2+1 нужно найти корни (x-1)(x^4-x^3+3x^2-x+1) , т.е. решить уравнение

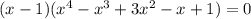
(x-1)(x^4-x^3+3x^2-x+1)=0

Тогда или х = - 1 или 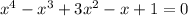x^4-x^3+3x^2-x+1=0

Решим это уравнение

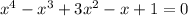
x^4-x^3+3x^2-x+1=0

так как х=0 не корень, то мы можем поделить на x² обе части уравнения

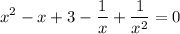
$\displaystyle x^2-x+3-\frac1x+\frac1{x^2}=0$

Тогда сделаем замену

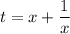
$\displaystyle t=x+\frac1x$

Тогда

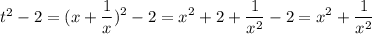
$t^2-2=\displaystyle (x+\frac1x)^2-2=x^2+2+\frac1{x^2}-2=x^2+\frac1{x^2}$

Преобразуем исходный многочлен

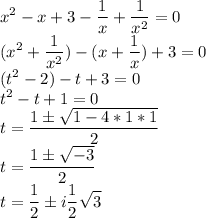
$\displaystyle x^2-x+3-\frac1x+\frac1{x^2}=0\\(x^2+\frac1{x^2})-(x+\frac1x)+3=0\\(t^2-2)-t+3=0\\t^2-t+1=0\\t=\frac{1\pm\sqrt{1-4*1*1}}{2}\\t=\frac{1\pm\sqrt{-3}}{2}\\t=\frac12\pm i\frac12\sqrt3$

Тогда сделаем обратную замену и решим для всех вариантов для t

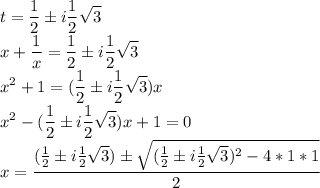
$\displaystyle t=\frac12\pm i\frac12\sqrt3\\x+\frac1x=\frac12\pm i\frac12\sqrt3\\x^2+1=(\frac12\pm i\frac12\sqrt3)x\\x^2-(\frac12\pm i\frac12\sqrt3)x+1=0\\x=\frac{(\frac12\pm i\frac12\sqrt3)\pm\sqrt{(\frac12\pm i\frac12\sqrt3)^2-4*1*1}}{2}\\$

Тогда есть 2 варианта:

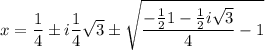
$\displaystyle x=\frac14\pm i\frac14\sqrt3\pm\sqrt{\frac{-\frac121-\frac12i\sqrt3}{4}-1}$

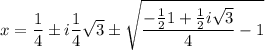
$\displaystyle x=\frac14\pm i\frac14\sqrt3\pm\sqrt{\frac{-\frac121+\frac12i\sqrt3}{4}-1}$

Тогда корни нашего исходного многочлена это

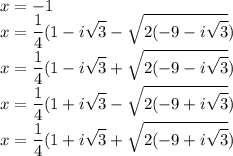
$\displaystyle x=-1\\x=\frac14(1-i\sqrt3-\sqrt{2(-9-i\sqrt3})\\x=\frac14(1-i\sqrt3+\sqrt{2(-9-i\sqrt3})\\x=\frac14(1+i\sqrt3-\sqrt{2(-9+i\sqrt3})\\x=\frac14(1+i\sqrt3+\sqrt{2(-9+i\sqrt3})$

4,6(32 оценок)

Это интересно:

12.09.2022

Искусство покорения сердец: как влюбить в себя парня...

Компьютеры-и-электроника

08.07.2020

Как скачать фильм с YouTube через YouTube Downloader...

Компьютеры-и-электроника

25.12.2021

Как правильно отправлять SQL запросы в Mysql из командной строки...

Хобби-и-рукоделие

29.03.2020