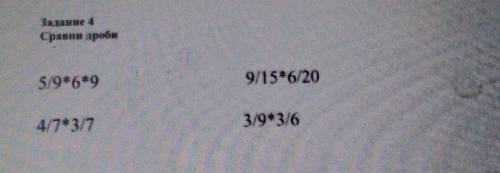
y=x^2-5x+6=(x-2)(x-3)
1) найти область определения функции; х∈r y∈r2) исследовать функцию на симметричность и периодичность;
непереодическая, f(x)≠-f(-x) f(x)≠ f(-x)
3)нули функции
х=0 у=0 y=0
у=6 х=2 x=3
4) асимптоты
k=lim(x-5+6/x)= ∞
асимптот нет
5) у`=2x-5=0
x=2.5(точка минимума)
y= 6.25-5*2.5+6=6.25-12.5+6=-0.25
6)у``=2
функция вогнутая на всем интервале.
7)график:
парабола, ветви вверх
вершина в (2.5; -0.25)
сам график:
Чтобы сравнить дроби, надо привести их к общему знаменателю.
5/9 и 6/9 знаменатель один, смотрим числитель.
5/9 > 6/9
.
.
9/15 и 6/20 общий знаменатель =60, но здесь удобнее сократить обе дроби.
9/15=3/5
6/20=3/10 (общий знаменатель = 10)
3/5=6/10,
6/10 > 3/10, значит
9/15 > 6/20
Если дроби не сокращать, то будет так
9/15=9/15 * 4/4=32/60
6/20=6/20 * 3/3=18/60
32/60 > 18/60.
.
.
4/7 и 3/7 - знаменатель один
4/7 > 3/7
.
.
3/9 и 3/6
Сократим дроби. (Чем меньше знаменатели, тем удобнее считать )))
3/9=1/3
3/6=1/2 общий знаменатель = 6.
1/3=2/6
1/2=3/6
2/6 < 3/6, значит
3/9 < 3/6.