
log₃(x+2) = 2 - |x|.
Задачу решаем графически.
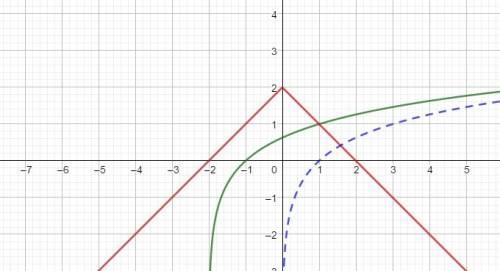
Рассмотрим функции у = log₃(x+2) и у = 2 - |x| и построим их графики.
1) у = log₃(x+2). Воспользуемся методом геометрических преобразований.
1. Строим график функции у = log₃(x) при x > 0;
2. Выполним параллельный перенос графика функции у = log₃(x) на 2 единицы влево и получим график функции у = log₃(x+2).
2) у = 2 - |x|. Также построим при метода геометрических преобразований.
1. Строим график функции у = 2 - x при x ≥ 0;
2. Отобразим график функции у = 2 - x при x ≥ 0 симетрично относительно оси ординат и получим график функции у = 2 - |x|. Графики во вложении. Ка видно из построения, данное уравнение имеет только одно решение.

99 - ( 15 + 36 + 9) = 99 - 60 = 39
125 125 125 125 125 125 125
13 - (22 - 19) = 13 - 3 = 10 = 1
50 50 50 50 50 50 5
47 + 25 - 60 = 72 - 60 = 12 = 4
99 99 99 99 99 99 33
362 + 102 - 400 = 464 - 400 = 64 = 16
700 700 700 700 700 700 175