ответ: 4) ≈0,9971; 5) 0,125.
Пошаговое объяснение:
4) пусть событие А состоит в том, что герб появится не более 8 раз. Рассмотрим противоположное событие В - герб появится 9 или 10 раз. Тогда, так как события А и В несовместны и притом образуют полную группу, P(A)+P(B)=1, откуда P(A)=1-P(B). Но P(B)=(1/2)⁹+(1/2)¹⁰≈0,0029. Отсюда P(A)≈1-0,0029=0,9971.
5) Событие А - из урны вынуты два шара одного цвета - может произойти совместно с одним из следующих событий, называемый гипотезами:
H1 - из урны вынуты 2 белых шара;
H2 - два чёрных шара.
Тогда A=H1*A+H2*A и по формуле полной вероятности p(A)=p(H1)*p(A/H1)+p(H2)*p(A/H2). А по формуле Байеса, p(H2/A)=p(H2)*p(A/H2)/p(A). Но p(H1)=7/10*6/9=42/90, p(H2)=3/10*2/9=6/90, p(A/H1)=p(A/H2)=1, так что p(H2/A)=6/90*1/(42/90*1+6/90*1)=1/8=0,125.
Павел Петрович, Александр Павлович, Николай Павлович, Александр Николаевич, Александр Александрович, Николай Александрович.
Пошаговое объяснение:
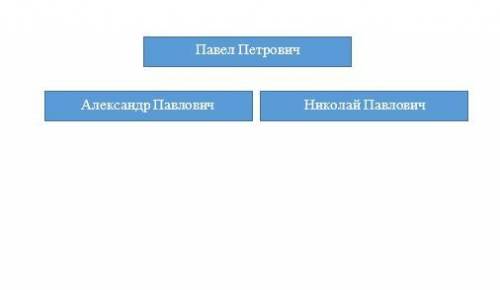
Павел Петрович не мог быть никому из них сыном или братом. У него одного только отчество Петрович. Значит он был первым. Тогда у него было два сына: Александр Павлович и Николай Павлович. См. рис.1
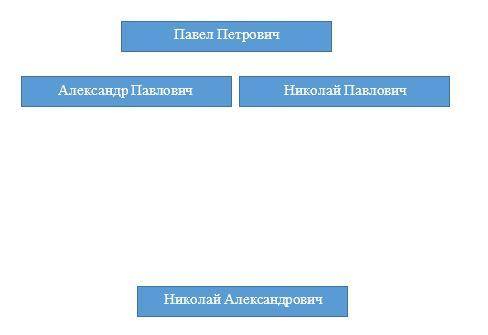
Последний был Николай. Николай Павлович, как выяснили, был или вторым, или третьим. Значит, последним был Николай Александрович. См. рис.2
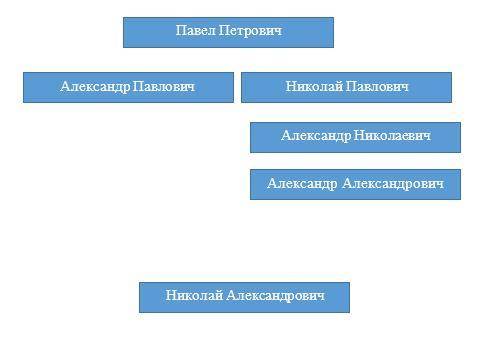
Осталось двое: Александр Александрович и Александр Николаевич. Если бы Александр Александрович был сыном Александр Павловича, то Александр Николаевич не мог бы быть его сыном. Значит, сын был у Николай Павловича. См. рис.3
Ну и поскольку сыновья следовали сразу за отцами, получаем окончательный порядок следования. См. рис.4

Вот решение. Клавиатура не может написать решение в столбик, поэтому я приложила фото. Думаю мой подчерк понятен.