S - расстояние, t - время, V - скорость
Первый поезд = П₁, второй поезд = П₂
П₁ и П₂ преодолевали S от пункта А в пункт В с разных концов, при этом V для П₁ = 120км/ч, V для П₂ = х км/ч и "общими усилиями" преодолели расстояние от А до В за 50мин (встретились через 50мин после того, как выехали). Далее они разъехались и П₁ прибыл в точку В на 75мин раньше, чем П₂ в точку А, значит t₁≠t₂ (общее время пути каждого поезда разное);
Внимание! Ещё раз повторюсь: за х мы взяли скорость П₂;
Формула: S(общ) = V(общ)*t (50мин=5/6часа);
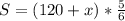

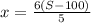
Допустим, поезда двигались одинаковое количество времени t₁=t₂; узнаем, на какое S П₁ проехал бы больше, чем П₂ (75мин=1,25часа):
120*1,25=150км
Т.е. поезда двигались бы одинаковое кол-во времени, если бы П₁ проехал ещё 150км с той же скоростью. Теперь, зная, что время движения поездов одинаковое (при S П₁ + 150км), возьмём их общее время за t.
 - выражение времени движения П₁.
- выражение времени движения П₁.
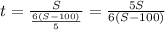 - выражение времени движения П₂.
- выражение времени движения П₂.
Поскольку под t в обоих выражениях подразумевается одно и тоже число, то и правые части выражений будут равны между собой. Запишем это:
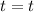 ⇔
⇔ 
Упростим полученное выражение (надеюсь, тему с решением рациональных уравнений Вы помните):


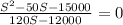
Правило: 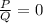 ⇔
⇔ 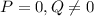
Перевод, если не понятно: дробь 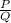 равна нулю, когда числитель P равен нулю, а знаменатель Q не равен нулю.
равна нулю, когда числитель P равен нулю, а знаменатель Q не равен нулю.
Следуя правилу, вычислим ОДЗ (область допустимых значений) - т.е. S|Q≠0 (такие значения S, при которых знаменатель Q не будет равен нулю):
120S-12000≠0
120S≠12000
S≠100 (посторонний корень)
Пояснение: если при решении уравнения один из корней будет = 100, то в ответ мы этот корень записать не сможем, т.к. при S=100 знаменатель Q равен нулю, а на нуль делить нельзя.
Теперь по правилу ищем S|Р=0 (такие значения S, при которых числитель Р будет равен нулю):

Решаем квадратное уравнение (ax²+bx+c=0);
Я сделаю через формулу частного случая при b - чётное число (  ):
):
 и
и 
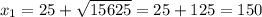
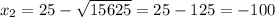
Пройденное расстояние не может быть отрицательным, х₂ нам не подходит. Значит, расстояние от пункта А до пункта В = 150км.
Из выше выведенной формулы для скорости вычислим V П₂;
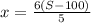 , подставляем значение S:
, подставляем значение S:
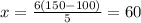
ответ: скорость второго поезда = 60км/ч.
Пошаговое объяснение:
Задача 1.
1. После понижения цены на 10%, билет станет стоить:
35*0,9=31,5 руб
2. На 120 рублей можно будет купить:
120:31,5=3,8 ⇒ 3 билета.
ответ: 3 билета.
Задача 2.
1. (4-3i)/(2+i)=(4-3i)(2-i)/(2+i)(2-i)=(8-4i-6i-3i²)/(4-i²). Т.к. i²=-1, делаем замену:
(8-10i-3*(-1))/(4-(-1))=(8-10i+3)/5=(5-10i)/5=5(1-2i)/5=1-2i
2. (1+i)³=1³+3*1²*i+3*1*i²+i³=1+3i+3i²+i³. Т.к. i²=-1, делаем замену:
1+3i+3*(-1)+(-1)*i=1+3i-3-i=-2+2i
3. i³-i¹⁰⁰=i²*i-(i²)⁵⁰. Т.к. i²=-1, делаем замену:
(-1)*i-(-1)⁵⁰=-i-1
Задача 2.
1. (17-6i)/(3-4i)=(17-6i)*(3+4i)/(3-4i)*(3+4i)=(51-18i+68i-24i²)/(9-16i²). Т.к. i²=-1, делаем замену:
(51-50i-24*(-1))/(9-16*(-1))=(75+50i)/25
2. (1-i)³= 1³-3*1²*i+3*1*i²-i³=1-3i+3i²-i³. Т.к. i²=-1, делаем замену:
1-3i+3*(-1)-(-1)*i=1-3i-3+i=-2i-2
3. i^40-i^21=(i²)²⁰-i²⁰⁺¹. Т.к. i²=-1, делаем замену:
(-1)²⁰-(-1)²⁰*i=(-1)²⁰*(1-i)=1*(1-i)=1-i
Задача 4.
Пусть х - производительность первого рабочего, у - производительность второго рабочего, тогда 60/х-60/у=3.
За один час оба рабочих производят Х+у деталей.
Составим систему уравнений:
60/х-60/у=3
х+у=30
Первое упростим, из второго уравнения выразим х:
60(х+у)/ху=3 ⇒ 20(х+у)=ху
х=30-у
Подставим в первое уравнение выраженный х, решим уравнение:
20(30-у-у)=у(30-у)
600-40у=30у-у²
у²-70у+600=0
Д-70*70-4*600=2500
у₁=(70-50)/2=10 х₁=30-10=20
у₂=(70+50)/2=60 х₂=30-60=-30 - не удовлетворяет условию
Время , за которое второй рабочий производит 90 деталей: 90/10=9 часов.
ответ: 9 часов
Задача 5.
Пусть х - количество десятков, у - количество единиц. Составим систему уравнений:
у-х=2
(х+у)*(10х+у)=280
Выразим из первого уравнения у и подставим во второе.
у=2+х
(х+2+х)(10х+2+х)=280
Решим получившееся уравнение:
(2х+2)(11х+2)=280
22х²+4х+22х+4=280
22х²+26х-276=0
Д=26²+4*22*276=24964=158²
х₁=(-26+158)/(2*22)=3
х₂=(-26-158)/(2*22) <0 - не удовлетворяет условию
у=2+3=5
Искомое число: 35
ответ: 35
Пусть скорость 2-ого велосипедиста Х км/ч, тогда скорость 1-ого = Х+10.
1-ый велосипедист проехал 20+45=65 км, а 2-ой всего лишь 45 км.
Оба велосипедиста затратили на свой путь одинаковое время.
Время 1-ого = 65/ (9Х+10); время 2-ого = 45/Х.
Составляем уравнение: 65 / (Х+10) = 45Х
65Х = 45(Х+10)
65 Х - 45Х = 450
20Х = 450
Х = 22,5
ответ: 22,5 км/час - скорость 2-ого велосипедиста.