1)2x=18
x=18/2=9
2)5x=15
x=15/5=3
3)9*a=18
a=18/9=2
4)58-20+c=40
38+c=40
c=40-38=2
5)14/c=2
c=14/2=7
6)c-(20+9)=60
c-29=60
c=60+29=89
Пошаговое объяснение:
y=3x^2-12x-15
Пошаговое объяснение:
Есть определенные правила нахождения производной. Например,в данном случае применяется правило (x^n). Производная будет равна nx^n-1
Применяя это правило например к первой части уравнения x^3 мы получаем 3x^2.
Может возникнуть вопрос,ууда делось (-2) в конце? Так вот,производная от любого числа равна 0!
Или же возникнет вопрос куда делся x в части (-15х)? Производная от х всегда =1
Для того,чтобы решать такие примеры нужна практика и знания производных
(Фото ниже)
Решаем дальше
В итоге мы имеем квадратное уравнение 3x^2-12x-15
Находим дискриминант = 18
х1=5 х2=-1
Думаю,это объяснять не нужно
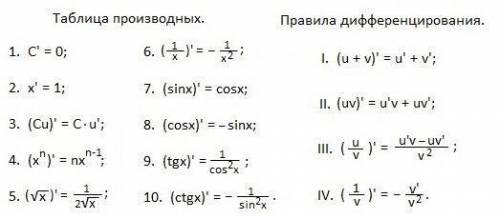
y=3x^2-12x-15
Пошаговое объяснение:
Есть определенные правила нахождения производной. Например,в данном случае применяется правило (x^n). Производная будет равна nx^n-1
Применяя это правило например к первой части уравнения x^3 мы получаем 3x^2.
Может возникнуть вопрос,ууда делось (-2) в конце? Так вот,производная от любого числа равна 0!
Или же возникнет вопрос куда делся x в части (-15х)? Производная от х всегда =1
Для того,чтобы решать такие примеры нужна практика и знания производных
(Фото ниже)
Решаем дальше
В итоге мы имеем квадратное уравнение 3x^2-12x-15
Находим дискриминант = 18
х1=5 х2=-1
Думаю,это объяснять не нужно
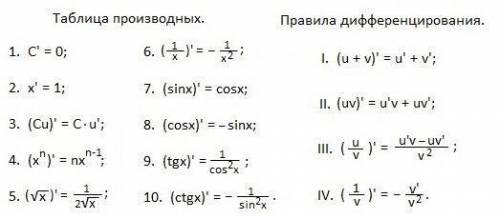
Пошаговое объяснение:
2х=18
х=18:2
х=9
15х=15
х=15:5
х=3
9а=18
а=18:9
а=2
58-20+с=40
38+с=40
с=40-38
с=2
14:с=2
с=14:2
с=7
с-(20+9)=60
с-29=60
с=60+29
с=89