1) На первое свободное место садится один из пяти (5 вариантов) на второе - один из четырех оставшихся (4 варианта), на третье - один из оставшихся трех (3 варианта), и т.д.
Всего вариантов = 5*4*3*2*1 = 120

2) Аналогично... первая цифра - одна из пяти (5 вариантов), вторая - одна из 4 оставшихся (4 варианта), на третьем - одна из трех последних (3 варианта). Всего
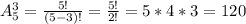
3) 10*9 = 90
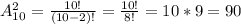
4) Вероятность, что ему достанется именно квартира на первом этаже - 6 вариантов из 90... = 6/90... Вероятность, что этого не случится P = 1 - 6/90 = 84/90
5) 3 мальчика из 8 = 8*7*6 = 336
2 девочки из 5 = 5*4 = 20
Всего вариантов = 336*20 = 6720
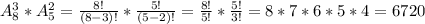
6) Всего различных чисел можно выложить = 4*3*2*1 = 24. Нас устраивает только один вариант... Вероятность = 1/24
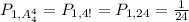
Рассмотрим эти же треугольники и покажем, что они равны:
1.<ВСА=<FМА
2. <АВС=<ЕМС
3. АМ = МС ( по св-ву медианы равнобедр. треуг.)
значит треугольники равны, а следовательно и их стороны. МF=ME
чтд