3
Пошаговое объяснение:
S=1/2+3/2²+5/2³+...+(2n - 3)/2ⁿ⁻¹+(2n - 1)/2ⁿ
2S=2(1/2+3/2²+5/2³+...+(2n - 1)/2ⁿ)=1+3/2+5/2²+...+(2n - 3)/2ⁿ⁻²+(2n - 1)/2ⁿ⁻¹
2S-S=(1+3/2+5/2²+...+(2n - 3)/2ⁿ⁻²+(2n - 1)/2ⁿ⁻¹)-(1/2+3/2²+5/2³+...+(2n - 3)/2ⁿ⁻¹+(2n - 1)/2ⁿ)
S=1+(3/2-1/2)+(5/2²-3/2²)+...+((2n - 1)/2ⁿ⁻¹-(2n - 3)/2ⁿ⁻¹)-(2n - 1)/2ⁿ=
=1+1+1/2+1/2²+1/2³+1/2⁴+...+1/2ⁿ⁻²-(2n - 1)/2ⁿ=
=1-(2n - 1)/2ⁿ+ (1+1/2+1/2²+1/2³+1/2⁴+...+1/2ⁿ⁻²)=1-(2n - 1)/2ⁿ+1·(1-(1/2)ⁿ⁻¹)/(1-1/2)=
=1-(2n - 1)/2ⁿ+2(1-1/2ⁿ⁻¹)=1-2n/2ⁿ+1/2ⁿ+2-1/2ⁿ⁻²=3-2n/2ⁿ-3/2ⁿ=3-(2n+3)/2ⁿ
Если последовательность бесконечная, то
S=1/2+3/2²+5/2³+...+(2n - 3)/2ⁿ⁻¹+(2n - 1)/2ⁿ+...=lim(n-->∞)[3-(2n+3)/2ⁿ]=3
Вычислим предел lim(n-->∞)[3-(2n+3)/2ⁿ]
lim(n-->∞)[3]-lim(n-->∞)[(2n+3)/2ⁿ]=3-lim(n-->∞)[(2n+3)/2ⁿ]
lim(n-->∞)[(2n+3)/2ⁿ] числитель и знаменатель дроби стремятся к ∞
Применим правило Лопиталя
Производная числителя 2
Производная знаменателя 2ⁿln2
lim(n-->∞)[(2n+3)/2ⁿ]=lim(n-->∞)[(2/(2ⁿln2)]=0
P.S.
Данным можно вычислить любую конечную последовательность вида:
S=a(1)·b(1)+a(2)·b(2)+a(3)·b(3)+...+a(n)·b(n)
Где числа a(1);a(2);a(3);..;a(n)-последовательные члены арифметической, а числа b(1);b(2);b(3);..;b(n)-геометрической прогрессии
Исаак Ньютон разработал метод извлечения квадратного корня, который восходил еще к Герону Александрийскому (около 100 г. н.э.). Метод этот (известный как метод Ньютона) заключается в следующем.
Пусть а1 — первое приближение числа (в качестве а1 можно брать значения квадратного корня из натурального числа — точного квадрата, не превосходящего х).
Следующее, более точное приближение а2 числа найдется по формуле: a2 = (1/2)*(a1 + (x/a1)).
Находим корень из 3.
Его точное (до 6 знаков) значение равно 1,732051.
а1 = 1.
а2 = (1/2)*(1 + (3/1) = 2.
а3 = (1/2)*(2 + 3/2) = 7/4 = 1,75.
а4 = (1/2)*((7/4) + 3/(7/4)) = 97/56 ≈ 1,732143.
Получено значение √3 = 1,732 с тремя верными знаками.
Находим корень из 7.
Его точное (до 6 знаков) значение равно 2,645751.
а1 = 2.
а2 = (1/2)*(2 + (7/2) = 11/4 =2,75.
а3 = (1/2)*(911/4) + 7/(11/4)) = 7/4 = 233/88 ≈ 2,647727.
а4 = (1/2)*((233/88) + 7/(233/88)) ≈ 2,645752.
Округляем полученное значение √7 = 2,646 до трёх знаков.
Сумма полученных значений равна 4,378.
Сумма более точных значений равна 4,377802.
Относительная погрешность равна:
(4,378 - 4,377802)/4,377802 = 4,52011E-05 или 0,005%.
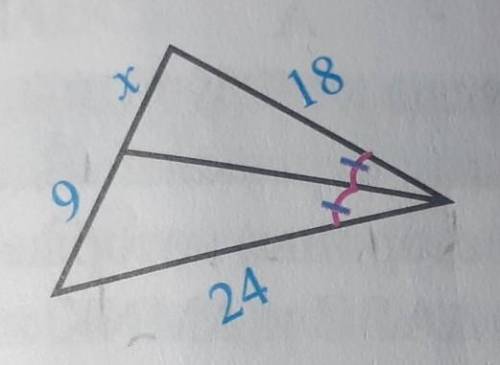
x=27/4
Пошаговое объяснение:
По свойству биссектрисы:
24/9=18/x
следовательно x= 27/4