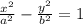 .
.
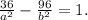

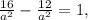
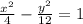
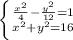
Вот как то так! Если не жалко сделай лучшим ответом и подпишитесь на меня и лайкните! С уважением Arolok!
SO_|_(ΔABC), O- центр правильного ΔАВС
центр правильного треугольника - точка пересечения медиан, биссектрис, высот, которые в точке пересечения делятся в отношении 2:1 считая от вершины.
высота правильного треугольника вычисляется по формуле:
h= \frac{a \sqrt{3} }{2}h=2a3
h=6√3*√3/2, h=9. OK=(1/3)*СК, ОК=3 см
SK_|_AB.
прямоугольный ΔSOK:<SOK=90°, SO=4 см, ОК=3 см
по теореме Пифагора:SK²=SO²+OK²
SK²=4²+3²
SK=5
ответ: расстояние от S до сторон правильного треугольника равно 5 см
21/9=х/12 => х=21*12/9=28л
2. Пусть основание треугольника - а, тогда противолежащий ему угол - А.
Найдём косинус угла А
sinA^2+cosA^2=1 => cosA^2= 1-0.36=0.64 => cosA=0.8
Через теорему косинусов найдём в и с, они равны (т. к. тр. равнобедренный) и обозначим их за х:
а^2=b^2+c^2-2*b*c*cosA
100=2x^2-2x^2*0.8
0,4*x^2=100
x=5√10 => b=c= 5√10
По формуле Герона найдём площадь:
p=(a+b+c)/2=(5+5√10)/2
S=√p(p-a)(p-b)(p-c)=75
3. 32sin2x+8cos4x=23 | cos4x=cos^2(2x)-sin^2(2x) |
32sin2x+8cos^2(2x)-8sin^2(2x)=23 | cos^2(2x)=1-sin^2(2x) |
32sin2x+8-8sin^2(2x)-8sin^2(2x)=23
sin2x=y составим уравнение:
-16y^2+32y-15=0
y1=1.25 y2=0.75
sin2x=1.25 sin2x=0.75