Пошаговое объяснение:
Испытания Бернулли: пусть есть n независимых испытаний, вероятность успеха в каждом из них равна p, вероятность неудачи q = 1 - p. Тогда вероятность того, что будет ровно k успехов равна C(n, k) p^k q^(n - k), где C(n, k) - биномиальный коэффициент C(n, k) = n! / (k! (n - k)!)
В обоих случаях будем искать вероятность того, что описанное в условии не произойдет - так проще.
а) Противоположное событие: произвошло меньше 4 неправильных соединений (т.е. 0, 1, 2 или 3).
P(не было неудачных) = (1 - 0,02)^150 = 0.98^150 = 0.0483
P(одно неудачное) = 150 * (1 - 0,02)^149 * 0.02 = 0.1478
P(два неудачных) = 150 * 149 / 2 * (1 - 0,02)^148 * 0.02^2 = 0.2248
P(3) = 150 * 149 * 148 / 6 * (1 - 0.02)^147 * 0.02^3 = 0.2263
P(<4) = 0.0483 + 0.1478 + 0.2248 + 0.2263 = 0.647
P(>=4) = 1 - 0.647 = 0.353
б) всё точно также, только не надо учитывать P(4).
P(<=2) = P(0) + P(1) + P(2) = 0.0483 + 0.1478 + 0.2248 = 0.421
P(>2) = 1 - 0.421 = 0.579
Можно сравнить точные результаты с приближенными. Тут можно вопрольззоваться теоремой Пуассона, P(k) = (np)^(-k) / k! * exp(-np).
Легко проверить, что в этом приближении P(<=2) = 0.423... (ошибка в третьем знаке после запятой), P(<=3) = 0.64723... (ошибка в пятом знаке)
3.
По условию, нам дан прямоугольный треугольник. Значит, один из его углов точно равен 90°.
Для удобства назовем треугольник ABC.
Пусть x - ∠C. Зная, что ∠A = 90°; ∠B = x + 20°, а также (по теореме внутренних углов) что сумма всех углов равна 180°, составим уравнение:
x + x + 20° + 90° = 180°
2x + 110° = 180°
2x = 70°
x = 70°:2
x = 35°
∠C = 35°.
∠B = ∠C + 20° = 35° + 20° = 55°
ответ: ∠1 - 55°, ∠2 - 35°.
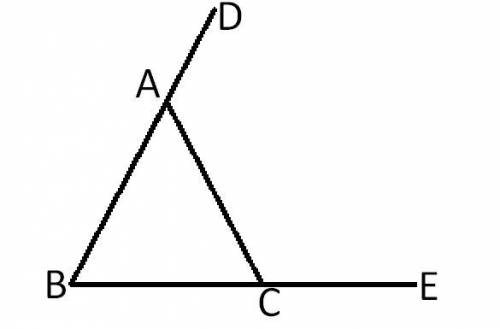
4.
Градусные меры внешних углов равны сумме углов, не смежных им. Снова для удобства назовём треугольник ABC, внешние углы - 145° - ∠DAC; 87° - ∠ACE (треугольник см. в приложении).
Зная, что смежные углы в сумме дают 180°, можно сказать, что
∠A = 180° - ∠DAC = 180° - 145° = 35°.
∠C = 180° - ∠ACE = 180° - 87° = 93°
∠B = 180° - ∠A - ∠C = 180° - 35° - 93° = 52°
ответ: ∠1 = 35°; ∠2 = 52°; ∠3 = 93°
Пошаговое объяснение:
1)
2)
3)
4)
5)
6)