Исключаем четвертого поставщика и меняем на 50% от первого завода.
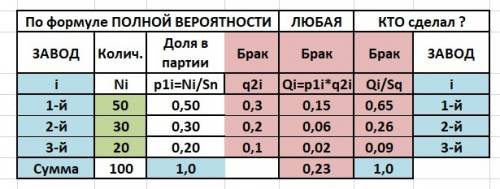
Решение сведено в таблицу. Таблица в приложении.
Задача состоит из двух событий - И случайно выбрать любой блок И этот блок - бракованный.
Вероятность выбора любого блока = Р1 - дана - (0,5 и 0,3 и 0,2).
Вероятность брака от любого завода = Р2 - дана - (0,3 и 0,2 и 0,1)
Вероятность события А - сумма произведений вероятностей каждого. Брак - это плохо - обозначаем Q.
Qi = 0.15(1зав) +0.06(2зав) +0.02(3зав) = 0.23 всего брак - ОТВЕТ а)
Вероятность кто изготовил этот брак находим по формуле Байеса.
Брак первого завода - 0,15 из 0,23 или 0,65 - ОТВЕТ б)
ДАНО: Y = (3x-1)/x
ИССЛЕДОВАНИЕ.
1. Область определения - Х≠0. Х∈(-∞;0)∪(0;+∞) - разрыв при Х=0.
2. Вертикальная асимптота: Х = 0.
3. Пересечение с осью Х.
3*х - 1 = 0 и х1 = 1/3
4. Пересечение с осью У - нет - не существует
5. Проверка на чётность.
Y(-x) = (3*x+1)/x ≠ - Y(x) ≠ Y(x) - ни чётная ни нечётная.
6, Поиск экстремумов через первую производную функции.
Запишем функцию Y(x) = (3x-1) * x⁻¹ - произведение двух функций.
Y'(x) = 3/x - (3*x-1)/x² = 0.
Корней - нет, Экстремумов - нет.
7. Интервалы монотонности.
Возрастает - Х∈(-∞;0)∪(0;+∞).
8. Из пункта 7 следует, что и точек перегиба нет.... КРОМЕ точки разрыва.
Вогнутая - "ложка" - Х∈(-∞;0) и выпуклая - "горка" - Х∈(0;+∞).
9. Горизонтальная асимптота - Y(-∞) = 3, Y(+∞)=3
Y = 3 - горизонтальная асимптота.
10. График в приложении.