
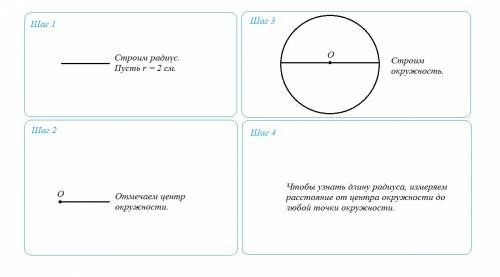
1) Строим отрезок, равный радиусу. Например, 2 см. То есть r = 2 см.
2) Отмечаем центр окружности (им будет край отрезка).
3) Измеряем циркулем отрезок, проводим окружность. Раствор циркуля должен оставаться неизменным.
4) Прикладываем линейку к радиусу и "продлеваем" его до пересечения с окружностью.
5) Чтобы узнать длину радиуса, нужно измерить расстояние от центра окружности до любой точки окружности.
упрощённый)
1) Берем произвольную длину радиуса. Пусть r = 2 см.
2) Так как радиус равен половине диаметра, то получаем следующее (вместо r подставляем значение радиуса):
d = 2r ⇒
d = 2·2 = 4 (см) - длина диаметра.
3) Отмечаем центр отрезка (диаметра). Это будет центр окружности.
Пусть O – центр окружности.
4) Строим окружность с центром в точке О.
5) Чтобы узнать длину радиуса, измеряем расстояние от центра окружности до любой точки окружности.
Синус обязан своему появлению на свет великому индийскому математику-астроному Ариабхату. Он оказал большое влияние на возникновение тригонометрии дав точное определение синусу, косинусу и арксинусу. В своих работах ученый назвал синус ардха-джа (ардха – половина, джа – тетива лука, которую напоминает хорда). Люди называли его просто джа.
Арабские математики изучили работу Ариабхаты, перевели её на арабский язык, после чего новым именем синуса стало джиба. Позже при переводе арабских математических текстов оно было заменено латинским синус (sinus – изгиб, кривизна).
Ариабхата был первым, кто разработал детализированные таблицы синуса и синус-верзуса (1 — cos x) с интервалом 3.75° от 0° до 90° и до 4-х знаков после запятой. Он использовал алфавитный код для определения интервала. При использовании таблицы Ариабхаты, было доказано правильное значение Sin30. Астрономические вычисления Ариабхаты подверглись некому влиянию арабов, которые обращались к его тригонометрическим таблицам для составления многих астрономических таблиц.
Это всё что я знаю