Пошаговое объяснение:
f(x) = x³-3x²-9x+7
условие существования критических точек f'(x₀)=0
условие возрастания убывания функции:
если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
итак, ищем первую производную
f'(x) = (x³)'-3(x²)'-9(x)'+(7) = 3x²- 6x - 9
ищем критические точки
3x²- 6x - 9 = 0, отсюда х₁ = -1, х₂ = 3
получили промежутки (-∞ ;-1) (-1; 3) (3; +∞) на каждом отрезке возьмем значение производной, в точке, близкой к критической и принадлежащей отрезку
(-∞ ;-1)
например точка х = -2
f'(-2) = 15 >0 - функция возрастает
(-1; 3)
например точка х=0
f'(0) = -9 <0 - функция убывает
(3; +∞)
например точка х=4
f'(4) = 15 >0 - функция возрастает
ответ
промежуток убывания (-1; 3)
Конус.
h (конуса) = R (конуса) = 7 см.
Найти:L - ? см.
S бок.поверх. - ? см².
Решение:Высота BO разделила равнобедренный ΔABC на два равных прямоугольных треугольника (их равенство можно доказать по всем признакам равенства прямоугольных треугольников, исходя из того, что ΔABC - равнобедренный).
Найдём гипотенузы этих прямоугольных треугольников по теореме Пифагора (c = a² + b², где c - гипотенуза, a и b - катеты):
AB = BC = √(7² + 7²) = √(49 + 49) = √98 = 7√2 cм.
S бок.поверх. = π * R * L = π * (7 * 7√2) = 49√2π см².
ответ: 7√2 см, 49√2π см².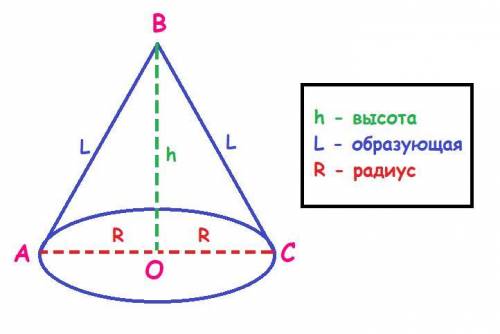
68,37-у=8,2*6,15
68,37-у=50,43
у=68,37-50,43
у=17,94