Пошаговое объяснение:
1.Найти произведение чисел 8 и 3.
8*3=24
2. Число, состоящее из 6 десятков 3 единиц уменьшить на частное чисел 27 и 3.
63-27:3=63-9=54
3. Сумму чисел 55 и 18 увеличить на произведение чисел 9 и 3.
(55+18)+9*3=73+27=100
4. Произведение чисел 9 и 2 увеличить на частное чисел 27 и 3.
9*2+27:3=18+9=27
5. Частное чисел 14 и 7 увеличить на 48.
14:7+48=50
6. Первое слагаемое 48, второе выражено произведением чисел 8 и 2. Чему равна сумма?
48+8*2=48+16=64
7. Число 80 уменьшить на произведение чисел 9 и 2.
80-9*2=80-18=62
8. Записать число, в котором не хватает 8 единиц до 9 десятков.
72 (72 + 8 единиц=9 десятков)
9. Разность чисел 13 и 7 умножить на 2.
(13-7)*2=12
10. В книге 18 страниц. Юра читал ежедневно по 6 страницы. За сколько дней Юра прочитал всю книгу?
18:6=3 дня
3. Решить уравнения:
14 : х= 7
х=14:7
х=2
14:2=7
х * 2 =18
х=18:2
х=9
9*2=18
24 : х =3
х=24:3
х=8
24:8=3
х : 3 = 4
х=3*4
х=12
12:3=4
х : 2= 10
х=10*2
х=20
20:2=10
Пусть 
грн стоит один килограмм апельсинов, а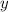 
грн — один килограмм лимонов. Тогда 5 кг апельсинов будут стоить 
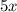грн, а 4 кг лимонов — 
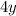грн, что вместе составляет 22 грн, то есть 
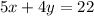. Также 6 кг апельсинов будут стоить 
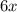грн, а 2 кг лимонов — 
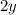грн, что вместе составляет 18 грн, то есть 
.
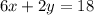Имеем систему из двух линейных уравнений:
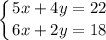
Домножим второе уравнение на 2:
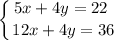
Вычтем из второго уравнения первое:
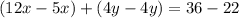
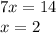
Тогда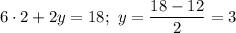 
Таким образом, 2 грн стоит один килограмм апельсинов и 3 грн стоит один килограмм лимонов.
ответ: 2 грн и 3 грн.
Найдём катеты: а = с·cosα, b = c·sinα.
При вращении вокруг гипотенузы с получаются два конуса, радиус основания которых R = c·cosα·sinα
Высота конуса, образующей которого является катет а = с·cosα, равна
h₁ = a·cosα = с·cosα·cosα = c·cos²α
Высота конуса, образующей которого является катет b = c·sinα, равна
h₂ = a·sinα = с·sinα·sinα = c·sin²α
Объём 1-го конуса:
V₁ = 1/3 πR²·h₁ = 1/3 ·π·(c·cosα·sinα)²·c·cos²α
Объём 2-го конуса:
V₂ = 1/3 πR²·h₂ = 1/3 ·π·(c·cosα·sinα)²·c·sin²α
Объём всего тела вращения:
V = V₁ + V₂ = 1/3 ·π·(c·cosα·sinα)²·c·cos²α + 1/3 ·π·(c·cosα·sinα)²·c·sin²α
= 1/3 ·π·(c·cosα·sinα)²·c·(cos²α + sin²α) = 1/3 ·π·c³·(cosα·sinα)² =
= 1/12 ·π·c³·(4cos²α·sin²α) = 1/12 ·π·c³·sin²2α