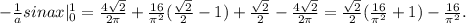2. Квадрат.
Пошаговое объяснение:
Точки M и M1 симметричны относительно некоторой точки O , если точка O является серединой отрезка MM1. Тогда точка O называется центром симметрии.
Для 2-фигуры, то есть для квадрата точка пересечения диагоналей будет центром симметрии (см. рисунок).
Точки M и M1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.
У квадрата четыре осей симметрии (см. рисунок).

Находим уравнение прямой:
Так как проходит через начало координат, то ищем в виде:
у = кх
Подставив координаты В:
п/4 = к
Итак уравнение прямой: у = пх/4.
Будем вычислять криволинейный интеграл (хотя в данном случае он - прямолинейный))) )исходя из того, что параметром будет х:
тогда :dy = y'dx = (п/4)dx
Получим:
I=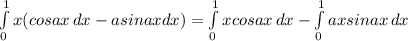
Здесь я обозначил:
а = П/4
Далее используя интегрирование по частям:
I=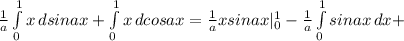
-