1)
(5/44+2/33)÷23/121 = (15/132+8/132)÷23/121 = 23/132÷23/121 = 11/12.
2)
Пропорция: 15 чел=3/8 части, х чел = 1 часть
Отсюда х=15÷3/8=40(чел) - сдавали всего;
40-15=25(чел) - не сдавали историю
3)
MF=FP=24÷2=12(см)
По т. Пифагора NF²=15²-12²=81; NF=9(см)
4)
2х²+5х-3=0
2х²+6х-х-3=0
2х(х+3)-(х+3)=0
(х+3)(2х-1)=0
х=-3; х=0,5
5)
х²(х-6)-9(х-6)<=0
(х²-9)(х-6)<=0
(х-3)(х+3)(х-6)<=0
Нарисовав "змейку", у тебя выйдет:
х∈(-∞; -6]∪[-3; 3]
6)
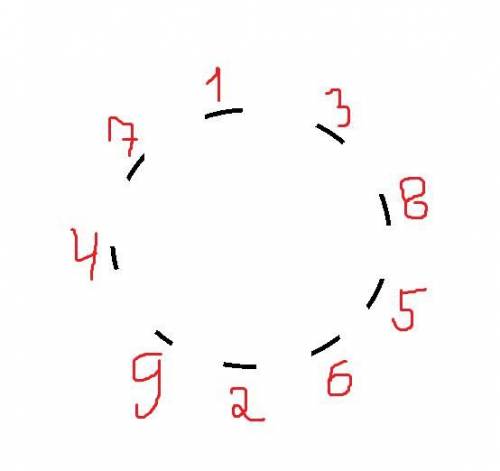
Всего у тебя 100 жетонов. Благоприятных условий 10 (7, 17, 27, 37, 47, 57, 67, 77, 87, 97). Верояность 10/100 = 1/10.
Да, можно
Пошаговое объяснение:
Максимально возможная сумма чисел — это 17 (8+9), а минимально — 3 (1+2). Теперь выясним, какие числа в этом диапазоне делятся на 3, 5 и 7. Это числа 3, 5, 6, 7, 9, 10, 12, 14, 15. Значит суммой чисел может быть 4, 8, 11, 13, 16, 17. Зная это, мы можем узнать, какие числа могут стоять рядом
с 1: 3, 7;
с 2: 6, 9;
с 3: 1, 5, 8;
с 4: 7, 9;
с 5: 3, 6, 8;
с 6: 2, 5, 7;
с 7: 1, 4, 6, 9;
с 8: 3, 5, 9;
с 9: 2, 4, 7, 8.
Если у числа только два "соседа", то оно обязательно будет стоять рядом с ними.
Теперь начнем выстраивать наш числовой круг. Начнем с единицы, так как у ней только один вариант возможных "соседей" (можно начинать с любого такого числа). Рядом с 7 обязательно будет стоять 4, а рядом с 4 — 9. Около 9 точно будет 2, а рядом с ней — 6. Теперь у нас осталось два числа — 5 и 8. Около 6 ставим 5, а около 3 — 8. 5 и 8 могут и будут стоять рядом, так как их сумма равна 13.
со второго 4х
с третьего 8х
с четвертого 4х так, как урожай со второго и четвертого участков равны
Составим уравнение
х+4х+8х+4х=1785
17х=1785
х=105 кг собрано с первого участка
4*105=420 кг собрано со второго и четвертого
8*105=840 кг собрано с третьего участка