Уравнение обязательно имеет одно решение: x = -4. Квадратное уравнение во второй скобке может иметь 0, 1 или 2 решения. Очевидно, нужно рассматривать последние два случая.
1. Если квадратное уравнение имеет одно решение, то оно должно отличаться от x = -4, так как требуется найти два различных решения.
2. Если квадратное уравнение имеет два решения, то одно из них должно равняться x = -4.
ОДЗ: {x>a {x>-a Проведем замену и получим уравнение t²-8at+12a²+8a-4=0 D=(4a-4)². Случай когда D=0 (a=1) нам не подходит, отметим это, во всех остальных случаях t1=6a-2 t2=2a+2 Теперь вернемся к замене Найдем x из первого уравнения: Проделав такую же штуку со вторым уравнением получим x_2=\frac{a(7^{2a+2}+1)}{7^{2a+2}-1} Нам нужно чтобы оба корня были решениями, то есть чтобы они принадлежали ОДЗ. Если а<0, то система которую я записал в самом начале равносильна неравенству x>-a Нам нужно чтобы оба корня принадлежали одз одновременно Решаем систему: {a<0 {x₁>-a {x₂>-a В этом случае получаем a<-1. Пусть теперь а>0, тогда система будет такая {a>0 {x₁>a {x₂>a Получаем а>1/3. Вспоминаем что a≠1 и объединяем решения. ответ: a∈(-oo; -1)∪(1/3; 1)∪(1;+oo)
и получим уравнение
12; 48
Пошаговое объяснение:
Уравнение обязательно имеет одно решение: x = -4. Квадратное уравнение во второй скобке может иметь 0, 1 или 2 решения. Очевидно, нужно рассматривать последние два случая.
1. Если квадратное уравнение имеет одно решение, то оно должно отличаться от x = -4, так как требуется найти два различных решения.
2. Если квадратное уравнение имеет два решения, то одно из них должно равняться x = -4.
Случай 1: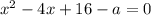
— 1 решение.
При a = 12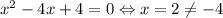
— подходит.
Случай 2: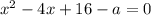
— 2 решения, одно из них x = -4.
При a = 48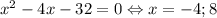
— подходит.