
Пошаговое объяснение:
Нехай швидкість човна х км/год, тоді
щвидкість за течією буде (х+4) км/год
швидкість проти течії (х-4) км/год
Відстань однакова 4 км ,
час за течією буде : 4/(х+4) год
проти течії 4/(х-4) год
за течією на 15 хв швидше
15 хв. = 15/60 = 1/4 години
Маємо рівняння :
4/(х-4)-4/(х+4)= 1/4 домножемо обидві сторони на 4
16/(х-4) - 16/(х+4)= 1
16(х+4)- 16*(х-4)=(х-4)(х+4)
16х+64-16х+64 = х²-16
х²-16=128
х²=128+16
х²=144
х₁=12 км/год
х₂=-12 - корінь не підходить , т ому що від "ємний
Отже власна швидкість човна 12 км/год
Если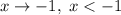 , то
, то 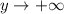 ; если
; если 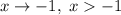 , то
, то 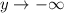
Если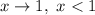 , то
, то 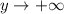 ; если
; если 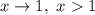 , то
, то 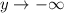
Найдем наклонные асимптоты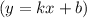 :
:
Если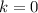 , то имеем горизонтальную асимптоту. Найдем
, то имеем горизонтальную асимптоту. Найдем 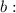
Следовательно,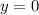 — горизонтальная асимптота.
— горизонтальная асимптота.
Из уравнения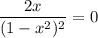 имеем критическую точку функции:
имеем критическую точку функции: 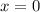
Заполним таблицу №1 (см. вложение).
Если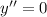 , то
, то 
Систематизируем данные, полученные по второй производной, в таблице №2 (см. вложение).
Для достоверности изобразим полученный график (см. вложение).