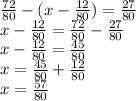
Примем скорость течения за Х км/ч. Тогда скорость по течению равна (20+х) км/ч и скорость против течения равна (20-х) км/ч. 60 км моторная лодка по течению за 60/(20+х) ч, и против течения – за 60/(20-х) ч. Так как на весь путь было затрачено 6,25 ч, составлю уравнение:
60/(20+х) + 60/(20-х) = 6,25
(60(20-х)+60(20+х)) / ((20-х)(20+х)) = 6,25
60(20-х)+60(20+х)-6,25(20-х)(20+х) / (20-х)(20+х) = 0
{ 1200-60х+1200+60х-6,25(400-х²) = 0
{ (20-х)(20+х)≠0
{ 2400-2500+6,25х² = 0
{ (20-х)(20+х)≠0
{ 6,25х²-100 = 0
{ (20-х)(20+х)≠0
{ х²-16 = 0
{ (20-х)(20+х)≠0
{ [х=–4: не подходит по условию задачи, ведь скорость течения не может быть отрицательной;
{ [х=4(км/ч)
{ (20-х)(20+х)≠0
ответ: 4 км/ч.
Пошаговое объяснение:
1. Найдите значение выражения:
а) раскрыв скобки: 28,3 + (–1,8 + 6) – (18,2 – 11,7) = 28,3 - 1,8 + 6 - 18,2 + 11,7 = 26
б) применив распределительное свойство умножения:
. 2. Упростите выражение:
а) 6 + 4а – 5а + а – 7а = -2a + 6
б) 5(п – 2) – 6(п + 3) – 3(2п – 9) = 5n - 10 - 6n - 18 - 6n + 27 = -7n - 1
в) .
3. Решите уравнение:
0,8(х – 2) – 0,7(х – 1) = 2,7.
0,8x - 1,6 - 0,7x + 0,7 = 2,7
0,1x - 0,9 = 2,7
0,1x = 2,7 + 0,9
0,1x = 3,6
x = 3,6 : 0,1
x = 36
4. Туристы путь в 270 км проделали, двигаясь 6 ч на теплоходе и 3 ч – на автобусе. Какова была скорость теплохода, если она вдвое меньше скорости автобуса?
6*x + 3*2x = 270
6x+6x = 270
12x = 270
x = 270 : 12
x = 22,5км/ч скорость теплохода
5. Найдите корни уравнения
(4,9 + 3,5х)(7х – 2,8) = 0.
4,9 + 3,5x = 0 или 7x - 2,8 = 0
3,5x = -4,9 7x = 2,8
x = -4,9 : 3,5 x = 2,8 : 7
x = -1,4 или x = 0,4
ответ: -1,4 ; 0,4
Подробнее - на -