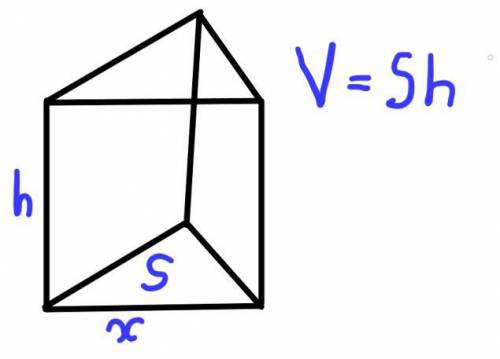21см²
сподіваюся правильно :)
Пусть функция y = f(x) непрерывна на отрезке [a; b] и F(x) - одна из первообразных функции на этом отрезке, тогда справедлива формула Ньютона-Лейбница: формула.
Формулу Ньютона-Лейбница называют основной формулой интегрального исчисления.
Для доказательства формулы Ньютона-Лейбница нам потребуется понятие интеграла с переменным верхним пределом.
Если функция y = f(x) непрерывна на отрезке [a; b], то для аргумента формула интеграл вида формула является функцией верхнего предела. Обозначим эту функцию формула, причем эта функция непрерывная и справедливо равенство формула.
Действительно, запишем приращение функции формула, соответствующее приращению аргумента формула и воспользуемся пятым свойством определенного интеграла и следствием из десятого свойства:
формула
где формула.
Перепишем это равенство в виде формула. Если вспомнить определение производной функции и перейти к пределу при формула, то получим формула. То есть, формула - это одна из первообразных функции y = f(x) на отрезке [a; b]. Таким образом, множество всех первообразных F(x) можно записать как формула, где С – произвольная постоянная.
Вычислим F(a), используя первое свойство определенного интеграла: формула, следовательно, формула. Воспользуемся этим результатом при вычислении F(b): формула, то есть формула. Это равенство дает доказываемую формулу Ньютона-Лейбница формула.
Приращение функции принято обозначать как формула. Пользуясь этим обозначением, формула Ньютона-Лейбница примет вид формула.
2
Пошаговое объяснение:
Пусть одна из сторон основания такой призмы - х, и ее высота - h. Тогда периметр ее боковой стороны -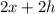 
и он равен 12.
Найдем объём такой призмы.
Объем призмы - площадь основания (в данном случае треугольника) умноженный на высоту (h)
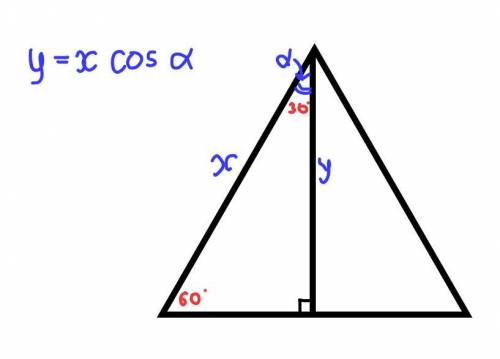
Найдём площадь треугольника в основании (см. рис. 1.)
1) проведём высоту у. Тогда площадь этого треугольника будет равна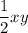 
После проведения высоты у нас оказался прямоугольный треугольник со сторонами x и y, и углом между ними в 30°
Тогда его площадь -
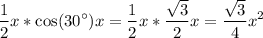
Выразим h через х: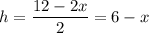 
Подставим в формулу объема:
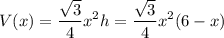
Найдём экстремумы функции:
1) Найдем производную:
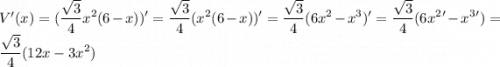
Приравняем её к 0
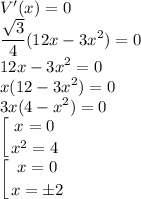
Поскольку у нас геометрия и таких страшных штук как отрицательные стороны у нас нет. Осталось только выбрать между 2 и 0.
Если 0, то это вообще не призма, знак производной говорит тоже самое.
Тогда подходит 2.
И это ответ!
