49.76 см²
Пошаговое объяснение:
Находим сначала площади круга и квадрата :
S=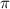
R² - площадь круга 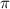≈3,14
S=a² - площадь квадрата
Площадь круга:
Нам известен диаметр d=8см
Если находить радиус через диаметр,то d=2R =>R=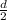
Вычислим радиус: R=8/2 => R=4 см
Теперь найдём площадь круга:
S=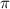*4² = 50.24 см²
Площадь квадрата:
Нам известно сторона a = 10 см
Из свойства квадрата : У квадрата все стороны равны ,поэтому:
S=10²=100 см²
Теперь найдём площадь закрашенной фигуры:
Sф=Sкв. - Sкруга => Sф=100 - 50.24 = 49.76 см²
Рассмотрим трёх подряд стоящих кенгуру с номерами 2 , 3 и 4 .
По условию, если второй кенгуру серый, то кенгуру 3 и 4 не серые ,
так как в любой произвольной тройке встречаются кенгуру всех трёх цветов .
Рассмотрим тройку кенгуру с номерами 3, 4 и 5 . Так как кенгуру 3 и 4 не серые , то пятый кенгуру серый и так далее . Таким образом кенгуру одного цвета образуют арифметическую прогрессию с разностью равной 3 . Пусть второй и 2021 -й кенгуру действительно серые .
Тогда должно выполняться равенство :
2 + 3(n - 1) = 2021 , где n - число кенгуру серого цвета . Отсюда :
3n = 2022 и n = 674 . Допустим что кенгуру под номером 1 красный .
Тогда 1 + 3(n - 1) = 202 , где n - число кенгуру красного цвета до
202 - го номера . Отсюда 3n = 204 и n = 68 .
Красный кенгуру не может быть третьим, так как тогда :
3 + 3(n - 1) = 202
n = 202 : 3 - не натуральное число .
Значит первый кенгуру красный, второй - серый, а третий синий, но тогда для синих кенгуру :
3 + 3(n - 1) = 20
n = 20 : 3 - не натуральное число .
Значит, Боря ошибся с двадцатым кенгуру, не угадав его цвет .
Допустим, что 20 - й кенгуру действительно синий, тогда синим будет и второй кенгуру, так как :
2 + 3(n - 1) = 20
n =21 : 3 = 7 - есть натуральное число .
Тогда Боря ошибся с серыми кенгуру с номерами 2 и 2021 .
Но, по условию он ошибся только один раз. Следовательно, серых и красных кенгуру он угадал правильно и ошибся с номером 20 .
ответ : 20