Построим все эти графики в одной системе координат (см. вложение №1). Получившаяся фигура не является криволинейной трапецией, но, проведя прямую (см. вложение №2), можно разбить её на две криволинейные трапеции, у каждой из которых можно найти площадь. Искомая площадь является суммой площадей двух составляющих эту фигуру криволинейных трапеций.
Итак, находим площадь левой криволинейной трапеции.
Теперь находим площадь правой криволинейной трапеции.
К началу XIV в. сильнейшими княжествами Севере-Восточной Руси стали Московское и Тверское. Первым московским князем по завещанию отца стал младший сын Александра Невского Даниил Александрович (1263 - 1303). В начале 90-х годов Даниил присоединил к Ростовскому княжеству Можайск, а в 1300 г. отвоевал у Рязани Коломну. Сын Даниила Юрий Данилович (ум. в 1324 г.) с 1304 г. повел борьбу за великое владимирское княжение с Михаилом Ярославичем Тверским, получившим в 1305 г. в Орде ярлык на великое княжение. Поддержку московскому князю оказывал митрополит всея Руси Петр. В 1317г. Юрий добился получения ярлыка на великокняжеский престол из рук хана Узбека, а спустя год в Орде главный враг Юрия - Михаил Тверской - был убит. Но в 1322 г. князь Юрий не выполнил волю хана и удержал при себе собранный ордынский "выход". В наказание за этот поступок хан лишил Юрия великого княжения, передав ярлык сыну Михаила Ярославича -Дмитрию Грозные очи. В 1325 г., когда московский и тверской князья находились в Орде, Дмитрий убил виновника гибели своего отца, князя Юрия, за что в 1326 г. был казнен ханом. Великое княжение было бpaту Дмитрия Тверского Александру (1326 - 1328). Вместе с великим князем Александром Тверским хан Узбек послал на Русь ордынский отряд во главе со своим родственником Чолханом (на Руси его называли Щелкан). Бесчинства ордынцев в Твери вызвали восстание горожан (1327), которое поддержал и сам князь Александр. Восставшие перебили отряд Чолхана. Эти события умело использовал новый московский князь, младший брат Юрия Даниловича Иван Калита. Он возглавил карательную ордынскую экспедицию на Тверь. Тверская земля была разорена, Александр Михайлович бежал во Псков, а великое владимирское княжение было поделено между Иваном Калитой и Александром Суздальским. После смерти последнего в 1332 г. ярлык на великое княжение почти постоянно находился в руках московских князей. Ивану Калите удалось упрочить свое влияние в Новгороде, приобрести в Орде ярлыки на удельные княжества с центрами в Угличе, Галиче и Белоозере. Помимо этого, Иван I покупал в других княжествах села, становившиеся опорными пунктами "собирания" русских земель вокруг Москвы. Политику Ивана Калиты продолжили его сыновья? Семен Гордый (1340?1353) и Иван II Красный (1353?1359). После смерти Ивана II Красного московским князем стал его 9-летний сын Дмитрий (1359?1389). В это время ярлыком на великое княжение завладел суздальско-нижегородский князь Дмитрий Константинович. Между ним и группировкой московского боярства развернулась острая борьба. На стороне Москвы выступал митрополит Алексий, фактически возглавлявший московское правительство, пока в 1363 г. победу окончательно не одержала Москва. Великий князь Дмитрий Иванович продолжал политику укрепления Московского княжества. В 1367 г. был возведен белокаменный Московский Кремль. В 1371 г. Москва нанесла сильное поражение рязанскому великому князю Олегу. Продолжалась борьба и с Тверью. Когда в 1371 г. Михаил Александрович Тверской, получив ярлык на великое княжение Владимирское, попытался занять Владимир, Дмитрий Иванович отказался повиноваться ханской воле. В 1375 г. Михаил Тверской вновь получил ярлык на владимирский стол. Тогда против него выступили почти все князья Северо-Восточной Руси, поддержав московского князя в его походе на Тверь. После месячной осады город капитулировал, по заключенному между московским и тверским князем договору Михаил признавал Дмитрия своим "братом старейшим", т. е. сюзереном. В результате внутриполитической борьбы в северо-восточных русских землях Московское княжество добилось первенствующего положения в "собирании" русских земель и превратилось в реальную силу противостоять Орде и Литве. С 1374 г. Дмитрий Иванович прекратил выплату дани Золотой Орде или нет не знаю! ну вот так!
Нужно вспомнить свойства четных/нечетных чисел. 1: при сложении или вычитании четных чисел получается четное число (10+32=42; 22-10=12). 2: при сложении или вычитании нечетных чисел получается четное число (13+15=28; 17-9=8) 3: при сложении или вычитании четного и нечетного чисел получается нечетное число (15+14=29; 31-10=21) 4: при умножении/делении четного на четное или четного на нечетное получается четное число. 5: при умножении/делении нечетных чисел получается нечетное число. Теперь решение. 100 и 50 - четные числа. т.е., на что бы мы их ни умножали (в целых числах), они останутся четными. Значит, исходная сумма четная. Андрею Крутому выдали 1999 купюр. Среди них достоинством в 1$, 5$, 25$. Чтобы получить четную сумму из этих купюр, их должно быть четное количество. Но их количество - 1999 купюр, а 1999 - число нечетное, значит, и выданная сумма нечетная. Исходная сумма - четная, а выданная - нечетная, т.е., отличается от исходной по крайней мере на 1. Стало быть, Андрея Крутого обсчитали.
Построим все эти графики в одной системе координат (см. вложение №1). Получившаяся фигура не является криволинейной трапецией, но, проведя прямую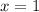 (см. вложение №2), можно разбить её на две криволинейные трапеции, у каждой из которых можно найти площадь. Искомая площадь является суммой площадей двух составляющих эту фигуру криволинейных трапеций.
(см. вложение №2), можно разбить её на две криволинейные трапеции, у каждой из которых можно найти площадь. Искомая площадь является суммой площадей двух составляющих эту фигуру криволинейных трапеций.
Итак, находим площадь левой криволинейной трапеции.
Теперь находим площадь правой криволинейной трапеции.
А теперь складываем и находим искомую площадь.
ответ: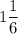 .
.