Есть гирлянда из 25 лампочек, изначально все лампочки не горят. Затем включается каждая первая лампочка (т. е. буквально каждая), потом выключается каждая вторая лампочка (начиная со второй), потом включается каждая третья, начиная с третьей, и т. д., в конце переключается каждая 25-я лампочка (т. е. последняя в ряду). Сколько лампочек останутся гореть после всех этих приключений?
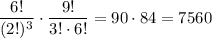
Число таких "хороших" семизначных чисел можно найти по формуле числа размещений из n по m (n - нижний индекс при A, m - верхний индекс при A):
A^m_n = n!/(n-m)!
(! - знак факториала)
A^3_9 = 9!/(9-3)!=9!/6!=7*8*9=504 - количество семизначных чисел, состоящих из 3 повторяющихся цифр (например, 7393937).
A^2_9 = 9!/(9-2)!=9!/7!=8*9=72 - количество семизначных чисел, состоящих из 2 повторяющихся цифр (например, 6636663)
A^1_9 = 9!/(9-1)!=9!/8!=9 - количество семизначных чисел, состоящих из 1 повторяющейся цифры (например, 8888888)
Всего таких чисел: A^3_9 + A^2_9 + A^1_9 = 504 + 72 + 9 = 585