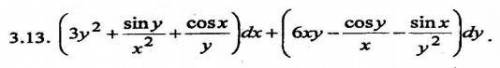
советую научиться пользоваться программой ПРОВОДНИК
Это основной файловый менеджер в системе Windows (любой версии)
Вы указали так называемый ПУТЬ К ФАЙЛУ
Откройте проводник, перейдите на КОМПЬЮТЕР, затем на диск С
И далее в его папки-подпапки
Users - Имя Пользователя - Downloads
А на будущее советую в вашем браузере (рискну предположить, что вы пользуетесь зайдите в настройки (справа-вверху три чёрточки) и в дополнительных параметрах в разделе ЗАГРУЗКИ поставьте галочку на пункте
«Запрашивать место для сохранения каждого файла перед загрузкой»
Тогда при попытке скачивания файла или сохранения картинки вам будет предлагаться указать папку с ОСМЫСЛЕННЫМ именем, где вы хотите хранить ваши загрузки.
Это обеспечит их сохранность на будущее.
А ваша скачанная картинка. которую вы не можете открыть, скорее всего погибла, т.к. была сохранена по умолчанию в бессмысленное место.
Пошаговое объяснение:
P(x;y)dx+Q(x;y)dy
является полным дифференциалом, если
∂P/∂y=∂Q/∂x.
∂P/∂y=((x+y)/(xy))`y=((x+y)`y·(xy)–(xy)`y·(x+y))/(xy)2= –x2/(xy)2= – 1/y2
∂Q/∂x=(1/y2)·(y–x)`x=(1/y2)·(–1)=–1/y2
∂P/∂y=∂Q/∂x
Данное уравнение – уравнение в полных дифференциалах
Это значит
∂U/∂x=P(x;y)
∂U/∂y=Q(x;y)
Зная, частные производные можем найти U(x;y)
U(x;y)= ∫ (∂U/∂x)dx= ∫ P(x;y)dx= ∫ (x+y)dx/(xy)=
=(1/y) ∫ (x+y)dx/x=(1/y) ∫ (1+(y/x))dx=(1/y)·x+(1/y)·yln|x|+ φ (y)=
=(x/y)+ln|x|+ φ(y)
Находим
∂U/∂y= ((x/y)+ln|x|+ φ(y))`y=x·(1/y)`+0+ φ `(y)= (–x/y2)+φ `(y)
Так как
∂U/∂y=Q(x;y)
то
(–x/y2)+φ `(y) =(y–x)/y2;
⇒
φ `(y)=1/y
φ(y)=ln|y|+C
U(x;y)=(x/y)+ln|x|+ φ(y)=(x/y)+ln|x|+ln|y|+C
О т в е т.U(x;y)=(x/y)+ln|x·y|+C