Математика: Решите уровнения б) 3,5х+2,2х=4,56 в) 3,2y-2,7у=0,6 г) 3,7z-z=0,54

Решите уровнения б) 3,5х+2,2х=4,56 в) 3,2y-2,7у=0,6 г) 3,7z-z=0,54

👇

Ответ:

Floki23

07.06.2021

Б)
3.5х+2.2х=4.56
5.7х=4.56
х=4.56:5.7
х=0.8
Проверка:
3.5+2.2*0.8=5.7*0.8=4.56

в)
3.2у-2.7у=0.6
0.5у=0.6
y=0.6:0.5
у=1.2
Проверка:
3.2-2.7*1.2=0.5*1.2=0.6

г)
3.7z-z=0.54
2.7z=0.54
z=0.54:2.7
z=0.2
Проверка:
3.7*0.2-0.2=0.74-0.2=0.54

Решите уровнения б) 3,5х+2,2х=4,56 в) 3,2y-2,7у=0,6 г) 3,7z-z=0,54

Решите уровнения б) 3,5х+2,2х=4,56 в) 3,2y-2,7у=0,6 г) 3,7z-z=0,54

4,7(80 оценок)

Открыть все ответы

Ответ:

natalyaepishenk

07.06.2021

Мясо и молоко.

Для получения молока и мяса лошадь используется с древнейших времен. Мясо молодых лошадей нежное, сочное, без привкуса, по химическому составу и калорийности незначительно отличается от говяжьего. Оно содержит 17 — 21% белка, до 23% жира, богато микроэлементами (кобальтом, йодом, медью) и витаминами. Убойный выход у лошадей высшей упитанности достигает 60%, средней — 48 — 52% и ниже средней — 45 — 48%. Конина, кроме употребления в свежем виде, широко используется для приготовления копченостей, колбас, консервов.

4,7(27 оценок)

Ответ:

sdfsdfsddf

07.06.2021

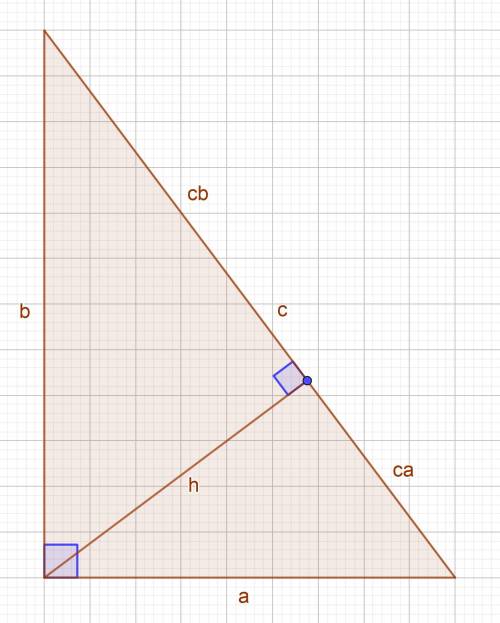
Обозначим катеты за a = 9 см, b = 12 см , гипотенузу за c, высоту за h, проекции катетов на гипотенузу за ca и ba.

Исходя из т. Пифагора, следует:

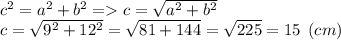
$c^2=a^2+b^2 = c=\sqrt{a^2+b^2} \\c = \sqrt{9^2+12^2}= \sqrt{81+144} = \sqrt{225} = 15 \:\: (cm)$

Найдет площадь прямоугольного треугольника:

$S = \frac{a\cdot b}{2} \\S = \frac{9\cdot 12}{2} = 9\cdot 6 = 54 \:\: (cm^2)$

Воспользуемся формулой площади треугольника через высоту и выразим из нее высоту:

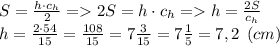
$S = \frac{h\cdot c_h}{2} = 2S = h\cdot c_h = h = \frac{2S}{c_h} \\h = \frac{2\cdot 54}{15} = \frac{108}{15}= 7\frac{3}{15} =7\frac{1}{5}=7,2 \:\: (cm)$

Проекции катетов будут равны:

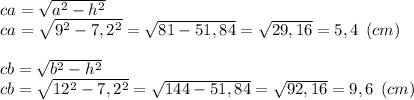
$ca = \sqrt{a^2-h^2} \\ca = \sqrt{9^2-7,2^2} = \sqrt{81-51,84}= \sqrt{29,16} = 5,4 \:\: (cm) \\\\cb = \sqrt{b^2-h^2} \\cb = \sqrt{12^2-7,2^2} = \sqrt{144-51,84}= \sqrt{92,16} = 9,6 \:\: (cm)$

или 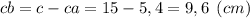$cb = c-ca = 15-5,4 = 9,6 \:\: (cm)$

—————————————————————————————

Высоту и проекции катетов также можно найти через пропорциональные отрезки в прямоугольном треугольнике:

– высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу:

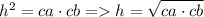
$h^2 = ca\cdot cb = h=\sqrt{ca\cdot cb}$

– катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:

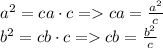
$a^2 = ca\cdot c = ca = \frac{a^2}{c} \\b^2 = cb\cdot c = cb = \frac{b^2}{c}\\\\$

—————————————————————————————

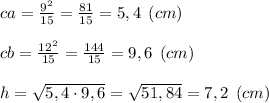
$ca=\frac{9^2}{15} = \frac{81}{15} = 5,4 \:\: (cm) \\\\cb=\frac{12^2}{15} = \frac{144}{15} = 9,6 \:\: (cm) \\\\h=\sqrt{5,4\cdot 9,6} =\sqrt{51,84} = 7,2 \:\: (cm)$