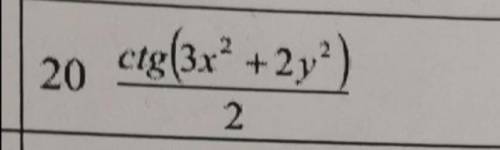
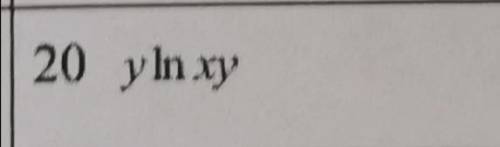
Площадь треугольника BOK равна KB*KO/2 (так как BKO прямой)
Угол OBK=альфа/2, так как BO биссектриса
Если обозначить точки касания на сторонах AB и AC через L и M соответственно и рассмотреть треугольники образованные точками касания, соседними вершинами треугольника и центром окружности, то окажется, что есть пары равных треугольников, из чего следует, что LB=KB, KC=MC, MA=LA. Подставляя эти равенства в LA+LB+KB+KC+MC+MA=2p, получаем 2MC+2MA+2KB=2p, откуда MC+MA+KB=p. С другой стороны, MC+MA=AC=a, поэтому KB=p-a
Тогда из треугольника OBK OB=KB*tg(альфа/2)=(p-a)*tg(альфа/2)
Подставляя в формулу для площади получим
S=((p-a)^2*tg(альфа/2))/2
1) x = 4,5
2) x = 32
3) x = 35
4) x = 13,125
5) x = 0,3
6) x = 3 3/14
7) x = 0,5
8) x = 1 29/96
Пошаговое объяснение:
1) x/16 = 9/32
32x = 9 * 16
32x = 144
x = 144/32
x = 4,5
2) 48/51 = x/34
51x = 48 * 34
51x = 1632
x = 1632/51
x = 32
3) 25/x = 5/7
5x = 25 * 7
5x = 175
x = 175/5
x = 35
4) 8/7 = 15/x
8x = 7 * 15
8x = 105
x = 105/8
x = 13,125
5) x : 1/2 = 3:5
x * 2/1 = 3/1 * 1/5
2x = 3/5
x = 3/5 : 2
x = 3/5 * 1/2
x = 3/10
x = 0,3
6) 3 : x = 14 : 15
3/x = 14/15
14x = 3 * 15
14x = 45
x = 45/14
x = 3 3/14
7) 3 : 4 = x : 2/3
3 : 4 = x * 3/2
3/4 = 3x/2
3x * 4 = 3 * 2
12x = 6
x = 6/12
x = 0,5
8) 144 : 125 = 1 1/2 : x
144 : 125 = 3/2 * 1/x
144/125 = 3/2x
2x * 144 = 125 * 3
288x = 375
x = 375/288
x = 125/96
x = 1 29/96
решение на фотографиях