Все четные числа кратны 2. Среди первых 1000 натуральных чисел четных и нечетных чисел поровну, т. е. количество и тех и других равно 1000/2 = 500. Нас интересуют все нечетные числа от 1 до 999. Их будет ровно 500. Далее, вторым условием является их некратность 5. В каждом десятке чисел 2 числа являются кратными 5. Т. к. 500 = 50*10, то у нас имеется 50 десятков и в каждом по два числа, кратных 5. Тогда число чисел не кратных ни 2, ни 5 будет 500 - 50*2 = 500 - 100 = 400. Добавим теперь условие некратности 3. В каждом десятке по три числа, кратных 3. У нас 400 чисел, т. е. 400 = 40*10 - 40 десятков. Среди них будет 40*3 = 120 чисел, кратных 3, значит всего чисел не кратных ни 2, ни 5, ни 3 будет 400 - 120 = 280.
ответ: 400 чисел некратных ни 2, ни 5 и 280 чисел некратных ни 2, ни 5, ни 3.
первый турист встретится со вторым Через 48 мин.
Пошаговое объяснение:
примем расстояние пройденное 1 туристом за "х" тогда: путь пройденный 2 туристом "АВ - х "
скорость 1 туриста v1 = АВ : 132 (m/min), время в пути 132 х : (АВ )
скорость 2 туриста v2 = АВ : 110 (m/min) время в пути 110(АВ -х) : (АВ)
первый вышел раньше на 22 мин.
Составляем уравнение: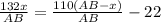 ( Домножим правую и левую часть на " АВ" ,
( Домножим правую и левую часть на " АВ" ,
132х = 110АВ - 110х - 22АВ
242х = 88 АВ
х = 88АВ : 242 = 4/11 * АВ Подставим в уравнение
t2 = 48 - 22 = 26 время в пути 2 туриста до встречи