1) Точка А = 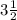 , а точка В =
, а точка В = 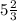 ⇒ расстояние между ними равно В - А
⇒ расстояние между ними равно В - А
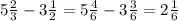
2) Натуральными числами называют целые числа, использующиеся при счёте
Нужно чтобы числа соответствовали неравенству 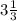 < x < 7
< x < 7
Т.к. 3<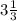 ⇒ нам нужна сумма чисел от 4 до 7, то есть 4 ≤ x < 7
⇒ нам нужна сумма чисел от 4 до 7, то есть 4 ≤ x < 7
4+5+6 = 15
3) Среднее арифметическое находится сложением данных чисел и делением их на их количество
а) 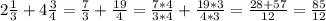
б) 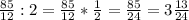
4) Действуем аналогично как в 3 задании
а) 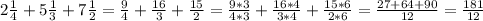
б) 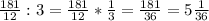
5) Действуем аналогично как в 2 задании
Нужно чтобы числа соответствовали неравенству 1 < x < 47,5
Т.к. 47,5 < 48 ⇒ нам нужно посчитать количество целых чисел от 1 до 47, то есть 1 < x ≤ 47
Их 46
1) Точка А = 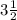 , а точка В =
, а точка В = 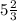 ⇒ расстояние между ними равно В - А
⇒ расстояние между ними равно В - А
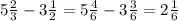
2) Натуральными числами называют целые числа, использующиеся при счёте
Нужно чтобы числа соответствовали неравенству 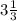 < x < 7
< x < 7
Т.к. 3<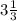 ⇒ нам нужна сумма чисел от 4 до 7, то есть 4 ≤ x < 7
⇒ нам нужна сумма чисел от 4 до 7, то есть 4 ≤ x < 7
4+5+6 = 15
3) Среднее арифметическое находится сложением данных чисел и делением их на их количество
а) 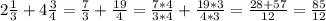
б) 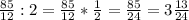
4) Действуем аналогично как в 3 задании
а) 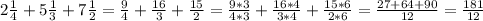
б) 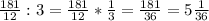
5) Действуем аналогично как в 2 задании
Нужно чтобы числа соответствовали неравенству 1 < x < 47,5
Т.к. 47,5 < 48 ⇒ нам нужно посчитать количество целых чисел от 1 до 47, то есть 1 < x ≤ 47
Их 46
1
2
3
4
5