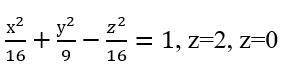
Я очень люблю своего дедушку. Мой дедушка — врач. Он давно должен быть на пенсии, но еще работает. На работе его с уважением называют по имени и отчеству, Виктором Борисовичем. Раньше он работал в больнице. Сейчас мой дедушка — участковый терапевт в поликлинике, он лечит взрослых людей и выписывает им больничные листы.
Дедушка Витя среднего роста. Я бы не назвал его худым или стройным. Скорее, он весьма упитанный человек. Дедушка носит усы. Голоса у него уже наполовину седая, и усы тоже. У дедушки густые черные с проседью брови и карие глаза.
С виду мой дед кажется добрым толстяком. Но он строгий и не даст себе «сесть на голову». Если дедушка сердится, его брови грозно хмурятся. В этот момент он может одним взглядом навести страху на того, кто с ним спорит. Пациенты и медсестры его очень уважают. А все внуки, то есть я и мои двоюродные братья, слушаются дедушку с первого раза.
Дедушка умеет делать все! У него золотые руки. Он может мастерить множество всяких вещей, даже мебель. Когда-то он сам собрал радиоприемник, потому что увлекался радио. Еще он когда-то хорошо играл на баяне, даже окончил музыкальную школу. Но потом забросил это дело, потому что стало некогда.
Мой дедушка — очень интересный человек. Я мог бы еще долго рассказывать о нем.
Do zagadnienia ochrony środowiska Białorusi należy zaliczyć zniknięcie wielu rzadkich gatunków, które jeszcze niedawno żyły republikę. Wśród nich fox, tur, drop, rosomak, soból, jesiotry i wiele innych. Dla zachowania gatunków zorganizowana duża liczba rezerwatów przyrody i biologicznych sanktuaria, a także prowadzona jest aktywna walka z kłusownicy.
Problemy ekologii muszą być kluczową kwestią dla wszystkich mieszkańców Białorusi. Tylko wspólnym wysiłkiem, a także na odpowiedzialnym odniesieniu do środowiska, można zachować przyrodę i przekazać jej bogactwo i piękno następnym pokoleniom.
Пошаговое объяснение:
здесь не будем заморачиваться тройными интегралами. посмотрим на наши поверхности
1 страшная формула - это однополостный гиперболоид
две других - это плоскости
объем тела, содержащегося между плоскостями z = а и z = Ь, выражается формулой:
плоскость, перпендикулярная оси Оz, в точке с аппликатой z пересекает гиперболоид по эллипсу
запишем наш эллипс
теперь нам надо каноническое уравнение нашего эллипса
упростим
площадь этого замечательного гиперболоида вычисляется по формуле
S=πab
у нас
отсюда
S=π*(3/4)(16+z²)
вот, собственно, и все "загогулины"
остался только объем