Пошаговое объяснение:
1.
Пусть скорость теплохода по озеру - х,
а скорость течения реки - у.
Принимаем расстояние, которое продходит теплоход за 1. ⇒
{1/х=4 {x=1/4 {x=1/4
{1/(x+y)=3 {x+y=1/3 {(1/4)+y=1/3 {y=(1/3)-(1/4)=(4-3)/12=1/12. ⇒
Скорость теплохода против течения:
x-y=(1/4)-(1/12)=(3-1)/12=2/12=1/6.
Время, за которое теплоход проходит то же расстояние против течения реки: 1/(1/6)=6 (час).
2.
Пусть собственная скорость лодки - х, а скорость течения реки - у.
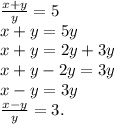
ответ: скорость лодки против течения реки больше скорости
течения реки в 3 раза.
Пошаговое объяснение:
1.
Пусть скорость теплохода по озеру - х,
а скорость течения реки - у.
Принимаем расстояние, которое продходит теплоход за 1. ⇒
{1/х=4 {x=1/4 {x=1/4
{1/(x+y)=3 {x+y=1/3 {(1/4)+y=1/3 {y=(1/3)-(1/4)=(4-3)/12=1/12. ⇒
Скорость теплохода против течения:
x-y=(1/4)-(1/12)=(3-1)/12=2/12=1/6.
Время, за которое теплоход проходит то же расстояние против течения реки: 1/(1/6)=6 (час).
2.
Пусть собственная скорость лодки - х, а скорость течения реки - у.
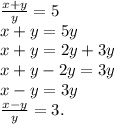
ответ: скорость лодки против течения реки больше скорости
течения реки в 3 раза.
Обозначим через х количество раз, которое нужно прибавить 5 к обоим числам, чтобы одно стало в 4 раза больше другого. Тогда первое число станет 145 + 5х. а второе число станет 10 + 5х. Чтобы уравнять эти числа, умножим меньшее на 4. Получим уравнение.
145 + 5х = 4 * (10 + 5х);
145 + 5х = 40 + 20х;
145 - 40 = 20х - 5х;
105 = 15х;
х = 105 : 15;
х = 7 раз.
145 + 5 * 7 = 180 - получится из первого числа.
10 + 5 * 7 = 45 - получится из второго числа.
180 в 4 раза больше 45.
ответ: 7 раз. 180 и 45.