Пошаговое объяснение:
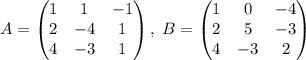
Здесь я позволю себе подробно расписать получение элементов при умножении матриц, но обычно все расчеты проводят усно и так лучше не шутить:)
а)
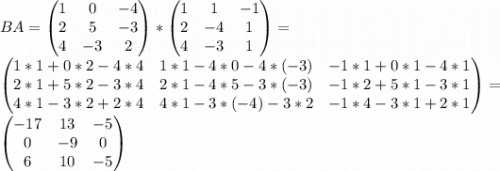
б)
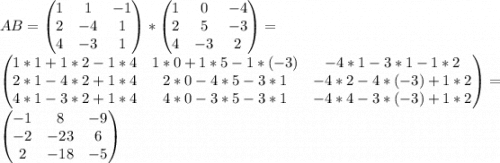
в) Перед поиском обратной матрицы проверим, существует ли она вообще. Поскольку обратные существуют только для невырожденных матриц, рассчитаем определитель и выясним, равен ли он нулю.
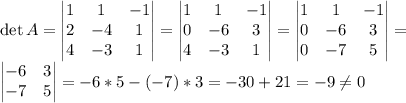
Итак, A^-1 существует. Найдем ее. Для начала транспонируем A:
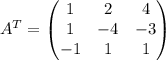
Теперь заменим каждый элемент на его минор и умножим полученную матрицу на число, обратное определителю. Я опять-таки сделаю все подробно, но повторять не стоит:)

Если мы сделали все правильно, то после умножения обратной матрицы на A (либо наоборот) получим единичную матрицу. Это как раз и предлагают провернуть в двух последних пунктах.
г)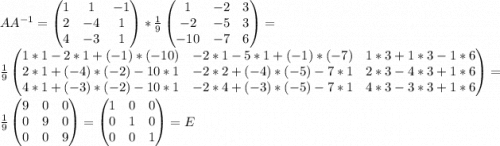 д)
д)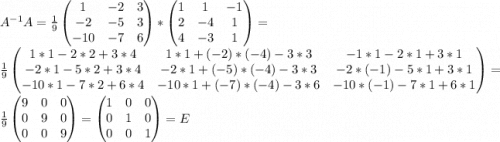
Т А К С
Т А К И
Т А С К
Т А С И
Т А И К
Т А И С
Т К А С
Т К А И
Т К С А
Т К С И
Т К И А
Т К И С
Т С А К
Т С А И
Т С К А
Т С К И
Т С И А
Т С И К
Т И А К
Т И А С
Т И К А
Т И К С
Т И С А
Т И С К
А Т К С
А Т К И
А Т С К
А Т С И
А Т И К
А Т И С
А К Т С
А К Т И
А К С Т
А К С И
А К И Т
А К И С
А С Т К
А С Т И
А С К Т
А С К И
А С И Т
А С И К
А И Т К
А И Т С
А И К Т
А И К С
А И С Т
А И С К
К Т А С
К Т А И
К Т С А
К Т С И
К Т И А
К Т И С
К А Т С
К А Т И
К А С Т
К А С И
К А И Т
К А И С
К С Т А
К С Т И
К С А Т
К С А И
К С И Т
К С И А
К И Т А
К И Т С
К И А Т
К И А С
К И С Т
К И С А
С Т А К
С Т А И
С Т К А
С Т К И
С Т И А
С Т И К
С А Т К
С А Т И
С А К Т
С А К И
С А И Т
С А И К
С К Т А
С К Т И
С К А Т
С К А И
С К И Т
С К И А
С И Т А
С И Т К
С И А Т
С И А К
С И К Т
С И К А
И Т А К
И Т А С
И Т К А
И Т К С
И Т С А
И Т С К
И А Т К
И А Т С
И А К Т
И А К С
И А С Т
И А С К
И К Т А
И К Т С
И К А Т
И К А С
И К С Т
И К С А
И С Т А
И С Т К
И С А Т
И С А К
И С К Т
И С К А
120
Пошаговое объяснение:
В дополнении к тому решению