y=-x^4+5x^2-4 - это квадратичная функция. График парабола, ветви вниз ( т.к. a=-1, a<0)
Найдем сначала x0 = -b/2a ( если забыли,квадратичное уравнение выглядит a^2 + bx -c = 0)
x0 = -5/2*1
Находим потом y0 подставив значение х в уравнение.
х0 и y0 - это центр функции. Т.е точка от куда будут идти пароболы
Потом находим нули функции. Это точки,которуые будут лежать на оси х и их будет пересекать данный график. Для этого решается данное квадратное уравнение : -x^4+5x^2-4=0 - обратная замена. Пусть t - x2
≈ 0.254
Пошаговое объяснение:
Пусть имеются следующие гипотезы:
H₁ - студенту попался вопрос на билет из 1 темы
H₂ - студенту попался вопрос на билет из 2 темы
H₃ - студенту попался вопрос на билет из 3 темы
H₄ - студенту попался вопрос на билет из 4 темы
Соответственно априорные вероятности тогда равны P(H₁)=P(H₂)=P(H₃)=P(H₄) =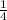 
Пусть событие A связано с тем, что студент не ответил на вопрос. Тогда условные вероятности равны:
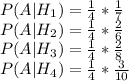
А полная вероятность (т.е. вероятность того, что студент не сдал экзамен) равна сумме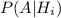 
по всем i.
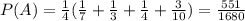
Находим теперь апостериорную вероятность, согласно формуле Байеса:
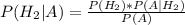
Таким образом,
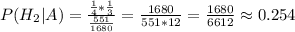
18,48:1,68-9,68)×0,2=0,264