190 прямых
Пошаговое объяснение:
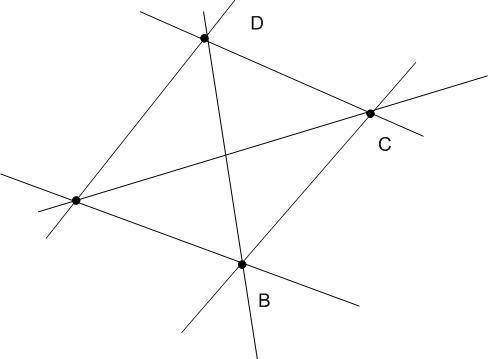
попробуем построить, ну, например для 4-х точек (см.рис).
Прямая проходит через каждые две точки. Т.е. нужно посчитать сколько различных пар точек можно выбрать из 4-х точек. Это - известная в комбинаторике формула для подсчета числа сочетаний (именно сочетаний, а не размещений, потому, что прямая АВ и прямая ВА - одна и таже прямая). Подсчитаем для 4-х точек:
C₄²=4!/(4-2)!4!=4!/(2!*2!)=3*4/2=6;
и действительно видим 6 прямых. Тогда для 20 точек:
C₂₀²=20!/((20-2)!2!)=19*20/2=190.
Пусть х - это длина одной стороны, тогда длина второй стороны будет равна (8-х)
Пусть у - площадь этого прямоугольника,
тогда у=х(8-х)
Требуется найти значение х, при котором у принимает максимальное значение
у=-х*х+8х график этой функции - парабола, у которой ветви направлены вниз и пересекают ось абцисс в точках, т.е. у=0, х=0 ; у=0, х=8
Значит максимум находится в вершине этой параболы. Значит х=4, а следовательно
одна сторона этого прямоугольника равна 4, а вторая сторона 8-4=4, это квадрат.
ответ: каждая стороны этого прямоугольника равна 4 метрам.
(5,1а+1,38)-3,4а=1,7а+1,38
при а=0,6 1,7*0,6+1,38=1,02+1,38=2,4
при а=1,8 1,7*1,8+1,38=3,06+1,38=4,44
Пошаговое объяснение: