ответ: a∈(-1;-2/3) ∪ (-2/3 ; -1/3)
Пошаговое объяснение:
ОДЗ: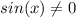 
Используем формулу:
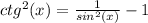
Замена: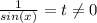 
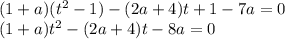
Заметим, что для того чтобы существовало одно решение на интервале (0;π/2), необходимо и достаточно, чтобы выполнялось условие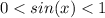 
, в этом случае на промежутке (0;π/2) будет существовать ровно ОДНО значение x, в противном случае, решений на данном промежутке не будет.
Откуда, должно выполнятся условие: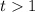 
По условию, нужно найти те значения параметра a, при которых будет более одного решения на интервале (0;π/2), а значит данное уравнение должно иметь как минимум два положительных решения.
1)
Рассмотрим линейный случай, ибо может быть бесконечное число решений: 
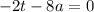- одно решение
2) Основной случай.
Должно быть два корня, каждый из которых больше единицы :
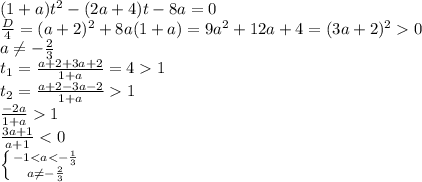
a∈(-1;-2/3) ∪ (-2/3 ; -1/3)
Решение простейших тригонометрических уравнений
Пример 1. Найдите корни уравнения
\[ \cos\left(4x+\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}, \]
принадлежащие промежутку [-\pi;\pi).
Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем k,\,n\in Z (на всякий случай, эта запись означает, что числа n и k принадлежат множеству целых чисел):
\[ 4x+\frac{\pi}{4}=\pm\operatorname{arccos \left(-\frac{\sqrt{2}}{2}\right)}+2\pi k. \]
Арккосинус a есть число, заключенное в интервале от 0 до \pi, косинус которого равен a.
Арксинус a есть число, заключенное в интервале от -\pi до \pi, косинус которого равен a.
Другими словами, нам нужно подобрать такое число из промежутка [0;2\pi], косинус которого был бы равен -\frac{\sqrt{2}}{2}. Это число \frac{3\pi}{4}. Используя это, получаем:
\[ 4x+\frac{\pi}{4} = \pm\frac{3\pi}{4}+2\pi k\Leftrightarrow \left[\begin{array}{l}x = \frac{\pi}{8}+\frac{\pi k}{2}, \\ x = -\frac{\pi}{4}+\frac{\pi n}{2}.\end{array}\right. \]
Потому что на 2 делятся чётные числа, а на 5 те, которые оканчиваются 5 или 0.
б) 10, 20, 30, 40, 50, 60, 70, 80, 90
Потому что на 10 делятся числа, которые оканчиваются нулём.
в) 15, 25, 35, 45, 55, 65, 75, 85, 95
Потому что на 5 делятся числа, которые оканчиваются 5 или 10, но в этом случае они не должны делится на 10. Поэтому только эти.